
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
分析 (1)由题中条件补充2×2列联表中的数据,
(2)利用2×2列联表中的数据,计算出k2,对性别与喜爱运动有关的程度进行判断,
(3)喜欢运动的女志愿者有6人,总数是从 这6人中挑两个人,而有4人会外语,求出满足条件的概率即可.
解答 解:(Ⅰ)
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 6 | 16 |
| 女 | 6 | 8 | 14 |
| 总计 | 16 | 14 | 30 |
点评 本题把概率的求法,列联表,独立性检验等知识有机的结合在一起,是一道综合性题目,但题目难度不大,符合新课标对本部分的要求,是道好题.


科目:高中数学 来源: 题型:解答题
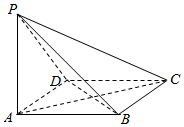 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥平面ABCD,PA=AB=AD=2,∠BAD=60°.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥平面ABCD,PA=AB=AD=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=f(x+2)的对称轴为x=-2 | B. | 函数y=f(2x)的对称轴为x=2 | ||
| C. | 函数y=f(x+2)的对称中心为(2,0) | D. | 函数y=f(2x)的对称中心为(2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB为圆O的直径,点C为圆O上的一点,且BC=$\sqrt{3}$AC,点D为线段AB上一点,且AD=$\frac{1}{3}$DB.PD垂直于圆O所在的平面.
如图,AB为圆O的直径,点C为圆O上的一点,且BC=$\sqrt{3}$AC,点D为线段AB上一点,且AD=$\frac{1}{3}$DB.PD垂直于圆O所在的平面.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方形ABCD与正方形ABEF构成一个$\frac{π}{3}$的二面角,将△BEF绕BE旋转一周.在旋转过程中,( )
如图,正方形ABCD与正方形ABEF构成一个$\frac{π}{3}$的二面角,将△BEF绕BE旋转一周.在旋转过程中,( )| A. | 直线AC必与平面BEF相交 | |
| B. | 直线BF与直线CD恒成$\frac{π}{4}$角 | |
| C. | 直线BF与平面ABCD所成角的范围是[$\frac{π}{12}$,$\frac{π}{2}$] | |
| D. | 平面BEF与平面ABCD所成的二面角必不小于$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 |
| y | $\frac{1}{2}$ | $\frac{3}{2}$ | 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -4 | C. | -6 | D. | -8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com