
分析 (1)根据三角函数诱导公式以及对数的运算性质计算即可;
(2)把根式内部的代数式化为平方的形式,然后计算得答案.
解答 解:(1)sin330°+5${\;}^{1-lo{g}_{5}2}$=sin(-30°)+$\frac{5}{2}$=-sin30°+$\frac{5}{2}$=2;
(2)$\sqrt{4-2\sqrt{3}}$+$\frac{1}{\sqrt{7+4\sqrt{3}}}$=$\sqrt{(1-\sqrt{3})^{2}}+\frac{1}{\sqrt{(2+\sqrt{3})^{2}}}$
=$\sqrt{3}-1+\frac{1}{2+\sqrt{3}}=\sqrt{3}-1+2-\sqrt{3}=1$.
故答案为:2,1.
点评 本题考查了三角函数的化简求值,考查了对数的运算性质,是基础题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{10}{3}$] | B. | [2,$\frac{10}{3}$] | C. | (2,+∞) | D. | [$\frac{10}{3}$,+∞] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
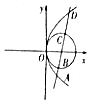 如图,抛物线C1:y2=2x和圆C2:(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$,其中p>0,直线l经过C1的焦点,依次交C1,C2于A,B,C,D四点,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值为$\frac{1}{4}$.
如图,抛物线C1:y2=2x和圆C2:(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$,其中p>0,直线l经过C1的焦点,依次交C1,C2于A,B,C,D四点,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值为$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2-x | B. | y=x-$\frac{1}{x}$ | C. | y=-$\frac{1}{{x}^{2}}$ | D. | y=-tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com