
ЎҫМвДҝЎҝОӘБЛСРҫҝЎ°НнЙПәИВМІиУлК§ГЯЎұУРОЮ№ШПөЈ¬өчІйБЛ100ГыИЛКҝЈ¬өГөҪПВГжөДБРБӘұнЈә
К§ГЯ | І»К§ГЯ | әПјЖ | |
НнЙПәИВМІи | 16 | 40 | 56 |
НнЙПІ»әИВМІи | 5 | 39 | 44 |
әПјЖ | 21 | 79 | 100 |
УЙТСЦӘКэҫЭҝЙТФЗуөГЈә![]() Ј¬ФтёщҫЭПВГжБЩҪзЦөұнЈә
Ј¬ФтёщҫЭПВГжБЩҪзЦөұнЈә
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
ҝЙТФЧціцөДҪбВЫКЗЈЁ Ј©
A. ФЪ·ёҙнОуөДёЕВКІ»і¬№э0.01өДЗ°МбПВИПОӘЎ°НнЙПәИВМІиУлК§ГЯУР№ШЎұ
B. ФЪ·ёҙнОуөДёЕВКІ»і¬№э0.01өДЗ°МбПВИПОӘЎ°НнЙПәИВМІиУлК§ГЯОЮ№ШЎұ
C. ФЪ·ёҙнОуөДёЕВКІ»і¬№э0.05өДЗ°МбПВИПОӘЎ°НнЙПәИВМІиУлК§ГЯУР№ШЎұ
D. ФЪ·ёҙнОуөДёЕВКІ»і¬№э0.05өДЗ°МбПВИПОӘЎ°НнЙПәИВМІиУлК§ГЯОЮ№ШЎұ

| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҙУДіРЈЖЪЦРҝјКФКэС§КФҫнЦРЈ¬ійИЎСщұҫЈ¬ҝјІміЙјЁ·ЦІјЈ¬Ҫ«Сщұҫ·ЦіЙ5ЧйЈ¬»жіЙЖөВК·ЦІјЦұ·ҪНјЈ¬НјЦРёчРЎЧйөДіӨ·ҪРОГж»эЦ®ұИҙУЧуЦБУТТАҙООӘ1:3:6:4:2Ј¬өЪТ»ЧйөДЖөКэКЗ4.

ЈЁ1Ј©ЗуСщұҫИЭБҝј°ёчЧй¶ФУҰөДЖөВКЈ»
ЈЁ2Ј©ёщҫЭЖөВК·ЦІјЦұ·ҪНј№АјЖіЙјЁөДЖҪҫщ·ЦәНЦРО»КэЈЁҪб№ыұЈБфБҪО»РЎКэЈ©.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘКэБР![]() өДКЧПоОӘ1Ј¬ЗТ
өДКЧПоОӘ1Ј¬ЗТ![]() Ј¬КэБР
Ј¬КэБР![]() ВъЧг
ВъЧг![]() Ј¬
Ј¬![]() Ј¬¶ФИОТв
Ј¬¶ФИОТв![]() Ј¬¶јУР
Ј¬¶јУР![]() .
.
ЈЁ1Ј©ЗуКэБР![]() Ўў
Ўў![]() өДНЁПКҪЈ»
өДНЁПКҪЈ»
ЈЁ2Ј©Бо![]() Ј¬КэБР
Ј¬КэБР![]() өДЗ°
өДЗ°![]() ПоәНОӘ
ПоәНОӘ![]() .Иф¶ФИОТвөД
.Иф¶ФИОТвөД![]() Ј¬І»өИКҪ
Ј¬І»өИКҪ![]() әгіЙБўЈ¬КФЗуКөКэ
әгіЙБўЈ¬КФЗуКөКэ![]() өДИЎЦө·¶О§.
өДИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэfЈЁxЈ©= ![]() Ј¬·ҪіМf2ЈЁxЈ©+mfЈЁxЈ©=0ЈЁmЎКRЈ©УРЛДёцІ»ПаөИөДКөКэёщЈ¬ФтКөКэmөДИЎЦө·¶О§КЗЈЁ Ј©
Ј¬·ҪіМf2ЈЁxЈ©+mfЈЁxЈ©=0ЈЁmЎКRЈ©УРЛДёцІ»ПаөИөДКөКэёщЈ¬ФтКөКэmөДИЎЦө·¶О§КЗЈЁ Ј©
A.ЈЁ©ҒЎЮЈ¬©Ғ ![]() Ј©
Ј©
B.ЈЁ©Ғ ![]() Ј¬0Ј©
Ј¬0Ј©
C.ЈЁ©Ғ ![]() Ј¬+ЎЮЈ©
Ј¬+ЎЮЈ©
D.ЈЁ0Ј¬ ![]() Ј©
Ј©
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДііЗКР![]() »§ҫУГсөДФВЖҪҫщУГөзБҝЈЁөҘО»Јә¶ИЈ©Ј¬ТФ
»§ҫУГсөДФВЖҪҫщУГөзБҝЈЁөҘО»Јә¶ИЈ©Ј¬ТФ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ·ЦЧйөДЖөВК·ЦІјЦұ·ҪНјИзНјЈ®
·ЦЧйөДЖөВК·ЦІјЦұ·ҪНјИзНјЈ®

ЈЁ1Ј©ЗуЦұ·ҪНјЦР![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©ЗуФВЖҪҫщУГөзБҝөДЦЪКэәНЦРО»КэЈ»
ЈЁ3Ј©ФЪФВЖҪҫщУГөзБҝОӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() өДЛДЧйУГ»§ЦРЈ¬УГ·ЦІгійСщөД·Ҫ·ЁійИЎ
өДЛДЧйУГ»§ЦРЈ¬УГ·ЦІгійСщөД·Ҫ·ЁійИЎ![]() »§ҫУГсЈ¬ФтФВЖҪҫщУГөзБҝФЪ
»§ҫУГсЈ¬ФтФВЖҪҫщУГөзБҝФЪ![]() өДУГ»§ЦРУҰійИЎ¶аЙЩ»§Јҝ
өДУГ»§ЦРУҰійИЎ¶аЙЩ»§Јҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіЙМіЎҫЩРРУРҪұҙЩПъ»о¶ҜЈ¬№ЛҝН№әВтТ»¶ЁҪр¶оөДЙМЖ·әујҙҝЙІОјУТ»ҙОійҪұ.ЛжЧЕійҪұ»о¶ҜөДУРР§ҝӘХ№Ј¬ІОУлійҪұ»о¶ҜөДИЛКэФҪАҙФҪ¶аЈ¬ёГЙМіЎ¶ФЗ°5МмійҪұ»о¶ҜөДИЛКэҪшРРНіјЖЈ¬yұнКҫөЪxМмІОјУійҪұ»о¶ҜөДИЛКэЈ¬өГөҪНіјЖұнИзПВЈә
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
ҫӯ№эҪшТ»ІҪНіјЖ·ЦОцЈ¬·ўПЦyУлxҫЯУРПЯРФПа№Ш№ШПө.
ЈЁ1Ј©ИфҙУХв5МмЛж»ъійИЎБҪМмЈ¬ЗуЦБЙЩУР1МмІОјУійҪұИЛКэі¬№э70өДёЕВКЈ»
ЈЁ2Ј©ЗлёщҫЭЙПұнМṩөДКэҫЭЈ¬УГЧоРЎ¶юіЛ·ЁЗуіцy№ШУЪxөДПЯРФ»Ш№й·ҪіМ![]() Ј¬Іў№АјЖёГ»о¶ҜіЦРш7МмЈ¬№ІУР¶аЙЩГы№ЛҝНІОјУійҪұЈҝ
Ј¬Іў№АјЖёГ»о¶ҜіЦРш7МмЈ¬№ІУР¶аЙЩГы№ЛҝНІОјУійҪұЈҝ
ІОҝј№«КҪј°КэҫЭЈә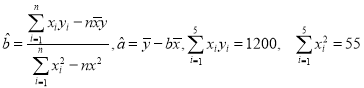 .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЦҙРРИзНјЛщКҫөДіМРтҝтНјәуЈ¬јЗЎ°Кдіц![]() КЗәГөгЎұОӘКВјюAЈ®
КЗәГөгЎұОӘКВјюAЈ®

ЈЁ1Ј©Иф![]() ОӘЗшјд
ОӘЗшјд![]() ДЪөДХыКэЦөЛж»ъКэЈ¬
ДЪөДХыКэЦөЛж»ъКэЈ¬![]() ОӘЗшјд
ОӘЗшјд![]() ДЪөДХыКэЦөЛж»ъКэЈ¬ЗуКВјюA·ўЙъөДёЕВКЈ»
ДЪөДХыКэЦөЛж»ъКэЈ¬ЗуКВјюA·ўЙъөДёЕВКЈ»
ЈЁ2Ј©Иф![]() ОӘЗшјд
ОӘЗшјд![]() ДЪөДҫщФИЛж»ъКэЈ¬
ДЪөДҫщФИЛж»ъКэЈ¬![]() ОӘЗшјд
ОӘЗшјд![]() ДЪөДҫщФИЛж»ъКэЈ¬ЗуКВјюA·ўЙъөДёЕВКЈ®
ДЪөДҫщФИЛж»ъКэЈ¬ЗуКВјюA·ўЙъөДёЕВКЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() Ј¬ЖдЦРКөКэ
Ј¬ЖдЦРКөКэ![]() Ј®
Ј®
ЈЁўсЈ©ЕР¶П![]() КЗ·сОӘәҜКэ
КЗ·сОӘәҜКэ![]() өДј«ЦөөгЈ¬ІўЛөГчАнУЙЈ»
өДј«ЦөөгЈ¬ІўЛөГчАнУЙЈ»
ЈЁўтЈ©Иф![]() ФЪЗшјд
ФЪЗшјд![]() ЙПәгіЙБўЈ¬Зу
ЙПәгіЙБўЈ¬Зу![]() өДИЎЦө·¶О§Ј®
өДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() .
.
ЈЁ1Ј©ЗуәҜКэ![]() өДЧоҙуЦөЈ»
өДЧоҙуЦөЈ»
ЈЁ2Ј©Иф¶ФУЪИОТв![]() Ј¬ҫщУР
Ј¬ҫщУР![]() Ј¬ЗуХэКөКэ
Ј¬ЗуХэКөКэ![]() өДИЎЦө·¶О§Ј»
өДИЎЦө·¶О§Ј»
ЈЁ3Ј©КЗ·сҙжФЪКөКэ![]() Ј¬К№өГІ»өИКҪ
Ј¬К№өГІ»өИКҪ![]() ¶ФУЪИОТв
¶ФУЪИОТв![]() әгіЙБўЈҝИфҙжФЪЈ¬Зуіц
әгіЙБўЈҝИфҙжФЪЈ¬Зуіц![]() өДИЎЦө·¶О§Ј»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙ.
өДИЎЦө·¶О§Ј»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com