练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，且bsinA= acosB． （Ⅰ）求角B的大小；
    （Ⅱ）若b=3，sinC=2sinA，求△ABC的面积．

    【答案】解：（Ⅰ）在△ABC中，∵bsinA= acosB， ∴由正弦定理可得 sinBsinA= sinAcosB．
    ∵sinA≠0，∴sinB= cosB，∴tanB= ，∴B= ．
    （Ⅱ）∵sinC=2sinA，∴c=2a，
    由余弦定理b2=a2+c2﹣2accosB，即9=a2+4a2﹣2a2acos ，
    解得a= ，c=2a=2 ．
    故△ABC的面积为 acsinB=
    【解析】（Ⅰ）在△ABC中，由 bsinA= acosB，利用正弦定理求得tanB的值，可得B的值．（Ⅱ）由条件利用正弦定理得c=2a，再由余弦定理b2=a2+c2﹣2accosB，求得a的值，可得c=2a的值，根据 △ABC的面积为 acsinB，计算求得结果．
    【考点精析】认真审题，首先需要了解正弦定理的定义(正弦定理:)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱中，，，，，点在线段上.

    （Ⅰ）证明；

    （Ⅱ）若是中点，证明平面；

    （Ⅲ）当时，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是矩形，平面平面分别为棱的中点.求证：

    （1）平面；

    （2）平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C所对边分别为a，b，c，已知 ． （Ⅰ）若b= ，当△ABC周长取最大值时，求△ABC的面积；
    （Ⅱ）设 的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2016高考北京文数】已知椭圆C：过点A（2,0），B（0,1）两点.

    （I）求椭圆C的方程及离心率；

    （Ⅱ）设P为第三象限内一点且在椭圆C上，直线PA与y轴交于点M，直线PB与x轴交于点N，求证：四边形ABNM的面积为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2017届湖南省长沙市高三上学期统一模拟考试文数】已知过的动圆恒与轴相切，设切点为是该圆的直径．

    （Ⅰ）求点轨迹的方程；

    （Ⅱ）当不在y轴上时，设直线与曲线交于另一点，该曲线在处的切线与直线交于点．求证: 恒为直角三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数
    （1）判断f（x）的单调性，说明理由．
    （2）解方程f（2x）=f﹣1（x）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对一批底部周长属于[80，130]（单位：cm）的树木进行研究，从中随机抽出200株树木并测出其底部周长，得到频率分布直方图如图所示，由此估计，这批树木的底部周长的众数是cm，中位数是cm，平均数是cm．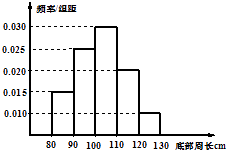

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动圆与圆： 相切，且与圆： 相内切，记圆心的轨迹为曲线.设为曲线上的一个不在轴上的动点， 为坐标原点，过点作的平行线交曲线于, 两个不同的点.

    （Ⅰ）求曲线的方程；

    （Ⅱ）试探究和的比值能否为一个常数？若能，求出这个常数，若不能，请说明理由；

    （Ⅲ）记的面积为， 的面积为，令，求的最大值.

    查看答案和解析>>

    同步练习册答案