
【题目】已知函数![]() ,其中
,其中![]() 为正实数.
为正实数.
![]() 讨论函数
讨论函数![]() 的单调性;
的单调性;
![]() 若存在
若存在![]() ,使得不等式
,使得不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】![]() 当
当![]() 时,在区间
时,在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;当
上单调递增;当![]() 时,在区间
时,在区间![]() 上单调递增;当
上单调递增;当![]() 时,在区间
时,在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;
上单调递增;![]()
![]() .
.
【解析】
![]() 由题意可知
由题意可知![]() 的定义域为
的定义域为![]() ,
,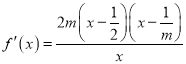 , 令
, 令![]() ,得
,得![]() ,
,![]() ,分类讨论
,分类讨论![]() ,
,![]() ,
,![]() 时导函数的正负来判断函数
时导函数的正负来判断函数![]() 的单调性;
的单调性;
![]() 若存在
若存在![]() ,使得不等式
,使得不等式![]() 成立,则
成立,则![]() 时,
时,![]() .由
.由![]() 可知,当
可知,当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() ;当
;当![]() ,即
,即![]() 时,由
时,由![]() 知
知![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,![]() ,当
,当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,![]() ,
,![]() 不成立,进而得出结论.
不成立,进而得出结论.
解:![]()
![]() 的定义域为
的定义域为![]() .
.
![]()
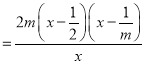 .
.
令![]() ,得
,得![]() ,
,![]() .
.
当![]() 时,即
时,即![]() 时,
时,
令![]() ,得
,得![]() ,或
,或![]() ;
;
令![]() ,得
,得![]() ,
,
故![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
当![]() 时,即
时,即![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 在区间
在区间![]() 上单调递增
上单调递增
当![]() 时,即
时,即![]() 时,令
时,令![]() ,得
,得![]() ,或
,或![]() ;
;
令![]() ,得
,得![]() ,故
,故![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
综上所述:当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
![]() 若存在
若存在![]() ,
,
使得不等式![]() 成立,
成立,
则![]() 时,
时,![]() .
.
由![]() 可知,当
可知,当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
![]() ,解得
,解得![]() ,
,
![]() ;
;
当![]() ,即
,即![]() 时,
时,
由![]() 知
知![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
![]()
![]() .
.
令![]() ,
,
![]() ,
,
则![]() ,
,
函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
![]() 恒成立,
恒成立,![]() .
.
当![]() ,即
,即![]() 时,
时,
函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
![]() ,
,![]() 不成立.
不成立.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为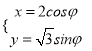 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求经过椭圆![]() 右焦点
右焦点![]() 且与直线
且与直线![]() 垂直的直线的极坐标方程;
垂直的直线的极坐标方程;
(2)若![]() 为椭圆
为椭圆![]() 上任意-点,当点
上任意-点,当点![]() 到直线
到直线![]() 距离最小时,求点
距离最小时,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点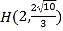 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)点![]() 在圆
在圆![]() 上,且
上,且![]() 在第一象限,过
在第一象限,过![]() 作
作![]() 的切线交椭圆于
的切线交椭圆于![]() 两点,问:
两点,问: ![]() 的周长是否为定值?若是,求出定值;若不是,说明理由.
的周长是否为定值?若是,求出定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司有两种发放薪水的方案:
方案一:底薪1800元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为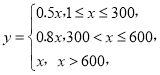
方案二:底薪2000元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为![]()
以下该公司某职工小甲在2019年9月份(30天)送快递的数据,
日送快递单数 | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)从小甲日送快递单数大于15的六天中抽取两天,求这两天他送的快递单数恰好都为16单的概率.
(2)请你利用所学的统计学知识为小甲9月份选择合适的发放薪水的方案,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球.规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得![]() 分,现从盒内任取3个球.
分,现从盒内任取3个球.
(Ⅰ)求取出的3个球中至少有一个红球的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设![]() 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市垃圾处理厂的垃圾年处理量(单位:千万吨)与资金投入量x(单位:千万元)有如下统计数据:
2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
资金投入量x(千万元) | 1.5 | 1.4 | 1.9 | 1.6 | 2.1 |
垃圾处理量y(千万吨) | 7.4 | 7.0 | 9.2 | 7.9 | 10.0 |
(1)若从统计的5年中任取2年,求这2年的垃圾处理量至少有一年不低于8.0(千万吨)的概率;
(2)由表中数据求得线性回归方程为![]() ,该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨,现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元,请你预测2017年能否完成垃圾处理任务,若不能,缺口约为多少千万吨?
,该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨,现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元,请你预测2017年能否完成垃圾处理任务,若不能,缺口约为多少千万吨?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,设
,设![]() ,则以下四个命题:(1)
,则以下四个命题:(1)![]() 是等差数列;(2)
是等差数列;(2)![]() 中最大项是
中最大项是![]() ;(3)
;(3)![]() 通项公式是
通项公式是![]() ;(4)
;(4)![]() .其中真命题的序号是______.
.其中真命题的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com