
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 作出f(x)的图象,由图象对各选项进行判断即可.x≤0时,$y=-{2}^{-x}+1=-(\frac{1}{2})^{x}+1$,可由$y=(\frac{1}{2})^{x}$的图象作关于x轴的对称图象,再向上平移一个单位得到.
解答 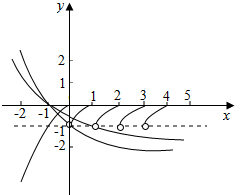 解:f(x)的图象如图所示:
解:f(x)的图象如图所示:
(1)∵f(-1)=-1≠f(0)=0,故(1)不正确;
(2)由图可知(2)正确;
(3)∵m=0时,f(m-1)=f(-1)=-1,不是最大值,故(3)不正确;
(4)如图(2)所示,图中两条曲线对应的a分别为$\frac{1}{3}$和$\frac{1}{2}$,故方程f(x)=loga(x+2)(0<a<1),有且只有两个实根,则a∈[$\frac{1}{3}$,$\frac{1}{2}$),故(4)正确.
∴正确命题的个数是2个.
故选:B.
点评 本题考查分段函数的性质、方程的根等知识,综合性较强,考查利用所学知识解决问题的能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [160,165) | 10 | 0.10 |
| [165,170) | 30 | 0.30 |
| [170,175) | a | 0.35 |
| [175,180) | b | c |
| [180,185] | 10 | 0.10 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com