
【题目】设函数f (x)=lnx-x+1.
(1)求f (x)的极值;
(2)若0<a<1,证明:函数g (x)=(x-a)ex-![]() ax2+a(a-1) x(x>lna)有极小值点x0,且g (x0)<0.
ax2+a(a-1) x(x>lna)有极小值点x0,且g (x0)<0.
【答案】(1)见解析;(2)见解析
【解析】
(1)求导数![]() ,解方程
,解方程![]() 列表检查
列表检查![]() 在
在![]() 的根
的根![]() 左右两侧值的符号,如果左正右负,那么
左右两侧值的符号,如果左正右负,那么![]() 在
在![]() 处取极大值,如果左负右正,那么
处取极大值,如果左负右正,那么![]() 在
在![]() 处取极小值;(2)令
处取极小值;(2)令![]() 得
得![]() ,
,![]() ,由(1)知
,由(1)知![]() ,可得
,可得![]() 有极小值点
有极小值点![]() ,只需证明
,只需证明![]()
![]()
![]() 即可.
即可.
(1)f′(x)的定义域为(0,+∞),f′(x)=![]() ,令f′(x)=0得x=1.
,令f′(x)=0得x=1.
当x变化时,f ′(x),f (x)的变化情况如下表:
x | (0,1) | 1 | (0,+∞) |
f ′(x) | + | 0 | - |
f (x) | ↗ | 极大 | ↘ |
所以当x=1时,f (x)取极大值f (1)=0,没有极小值.
(2)g′(x)=(ex-a)[ x-(a-1)],令g′(x)=0得x1=lna,x2=a-1.
因为0<a<1,由(1)知lna<a-1.
当x∈(lna,a-1)时,g′(x)<0;当x∈(a-1,+∞)时,g′(x)>0;所以g (x)有极小值点x0=a-1.
由lna<a-1,得ea-1>a.
g (x0)=g (a-1)=![]() a(a-1)2-ea-1<
a(a-1)2-ea-1<![]() a(a-1)2-a=
a(a-1)2-a=![]() a(a2-2a-1).
a(a2-2a-1).
因为0<a<1,所以a2-2a-1<0,因此g (x0)<0.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:
年龄x | 28 | 32 | 38 | 42 | 48 | 52 | 58 | 62 |
收缩压 | 114 | 118 | 122 | 127 | 129 | 135 | 140 | 147 |
其中: ,
,![]() ,
,![]()

![]() 请画出上表数据的散点图;
请画出上表数据的散点图;
![]() 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;![]() 的值精确到
的值精确到![]()
![]() 若规定,一个人的收缩压为标准值的
若规定,一个人的收缩压为标准值的![]() 倍,则为血压正常人群;收缩压为标准值的
倍,则为血压正常人群;收缩压为标准值的![]() 倍,则为轻度高血压人群;收缩压为标准值的
倍,则为轻度高血压人群;收缩压为标准值的![]() 倍,则为中度高血压人群;收缩压为标准值的
倍,则为中度高血压人群;收缩压为标准值的![]() 倍及以上,则为高度高血压人群
倍及以上,则为高度高血压人群![]() 一位收缩压为180mmHg的70岁的老人,属于哪类人群?
一位收缩压为180mmHg的70岁的老人,属于哪类人群?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “f(0)![]() ”是“函数f(x)是奇函数”的充要条件
”是“函数f(x)是奇函数”的充要条件
B. 若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]()
C. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
D. 若![]() 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且当点
两点,且当点![]() 是椭圆
是椭圆![]() 的上顶点时,
的上顶点时,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)延长线段![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,若
,若![]() ,求此时
,求此时![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次投篮测试中,有两种投篮方案:方案甲:先在A点投篮一次,以后都在B点投篮;方案乙:始终在B点投篮.每次投篮之间相互独立.某选手在A点命中的概率为![]() ,命中一次记3分,没有命中得0分;在B点命中的概率为
,命中一次记3分,没有命中得0分;在B点命中的概率为![]() ,命中一次记2分,没有命中得0分,用随机变量
,命中一次记2分,没有命中得0分,用随机变量![]() 表示该选手一次投篮测试的累计得分,如果
表示该选手一次投篮测试的累计得分,如果![]() 的值不低于3分,则认为其通过测试并停止投篮,否则继续投篮,但一次测试最多投篮3次.
的值不低于3分,则认为其通过测试并停止投篮,否则继续投篮,但一次测试最多投篮3次.
(1)若该选手选择方案甲,求测试结束后所得分![]() 的分布列和数学期望.
的分布列和数学期望.
(2)试问该选手选择哪种方案通过测试的可能性较大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知a,b,N都是正数,a≠1,b≠1,证明对数换底公式:logaN=![]() ;
;
(2)写出对数换底公式的一个性质(不用证明),并举例应用这个性质.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,错误的是( )
A. 在![]() 中,
中, ![]() 则
则![]()
B. 在锐角![]() 中,不等式
中,不等式![]() 恒成立
恒成立
C. 在![]() 中,若
中,若![]() ,则
,则![]() 必是等腰直角三角形
必是等腰直角三角形
D. 在![]() 中,若
中,若![]() ,
, ![]() ,则
,则![]() 必是等边三角形
必是等边三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 的圆
的圆![]() 的圆心
的圆心![]() 在
在![]() 轴的非负半轴上,且圆
轴的非负半轴上,且圆![]() 截直线
截直线![]() 所得弦长为
所得弦长为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我市参加2018年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成![]() 六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
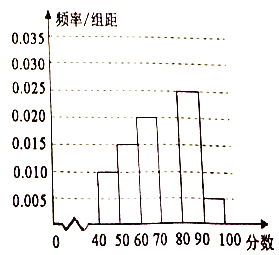
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数、均值;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要所少分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com