
【题目】已知函数f(x)=x2+ex﹣ ![]() (x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(﹣∞, ![]() )
)
D.(﹣∞, ![]() )
)
【答案】C
【解析】解:由题意,存在x<0,
使f(x)﹣g(﹣x)=0,
即ex﹣ ![]() ﹣ln(﹣x+a)=0在(﹣∞,0)上有解,
﹣ln(﹣x+a)=0在(﹣∞,0)上有解,
令m(x)=ex﹣ ![]() ﹣ln(﹣x+a),
﹣ln(﹣x+a),
则m(x)=ex﹣ ![]() ﹣ln(﹣x+a)在其定义域上是增函数,
﹣ln(﹣x+a)在其定义域上是增函数,
且x→﹣∞时,m(x)<0,
若a≤0时,x→a时,m(x)>0,
故ex﹣ ![]() ﹣ln(﹣x+a)=0在(﹣∞,0)上有解,
﹣ln(﹣x+a)=0在(﹣∞,0)上有解,
若a>0时,
则ex﹣ ![]() ﹣ln(﹣x+a)=0在(﹣∞,0)上有解可化为
﹣ln(﹣x+a)=0在(﹣∞,0)上有解可化为
e0﹣ ![]() ﹣ln(a)>0,
﹣ln(a)>0,
即lna< ![]() ,
,
故0<a< ![]() .
.
综上所述,a∈(﹣∞, ![]() ).
).
故选:C
【考点精析】本题主要考查了函数的图象的相关知识点,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1,点M与曲线C的焦点不重合,若点M关于曲线C的两个焦点的对称点分别为A,B,M,N是坐标平面内的两点,且线段MN的中点P恰好在双曲线C上,则|AN﹣BN|= .
=1,点M与曲线C的焦点不重合,若点M关于曲线C的两个焦点的对称点分别为A,B,M,N是坐标平面内的两点,且线段MN的中点P恰好在双曲线C上,则|AN﹣BN|= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x2﹣6x+5≤0,q:x2﹣2x+1﹣m2≤0(m>0).
(1)若m=2,且p∧q为真,求实数x的取值范围;
(2)若p是q充分不必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆E:(x+ ![]() )2+y2=16,点F(
)2+y2=16,点F( ![]() ,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q. 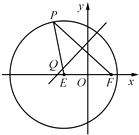
(1)求动点Q的轨迹Γ的方程;
(2)设直线l与(1)中轨迹Γ相交于A,B两点,直线AO,l,OB的斜率分别为k1 , k,k2(其中k>0),若k1 , k,k2恰好构成公比不为1的等比数列,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一四棱锥P﹣ABCD的三视图如图所示,E是侧棱PC上的动点. 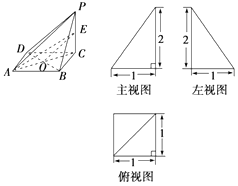
(Ⅰ)求四棱锥P﹣ABCD的体积.
(Ⅱ)若点E为PC的中点,AC∩BD=O,求证:EO∥平面PAD;
(Ⅲ)是否不论点E在何位置,都有BD⊥AE?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 2 | ﹣2 | 0 |
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;
(2)将函数y=f(x)的图象向左平移 ![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com