
【题目】已知项数为![]() 的数列
的数列![]() 满足如下条件:①
满足如下条件:①![]() ;②
;②![]() .若数列
.若数列![]() 满足
满足![]() ,其中
,其中![]() ,则称
,则称![]() 为
为![]() 的“伴随数列”.
的“伴随数列”.
(1)数列1,3,5,7,9是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
(2)若![]() 为
为![]() 的“伴随数列”,证明:
的“伴随数列”,证明:![]() ;
;
(3)已知数列![]() 存在“伴随数列”
存在“伴随数列”![]() ,且
,且![]() ,
,![]() ,求m的最大值.
,求m的最大值.
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】给出下列六个命题:
(1)若![]() ,则函数
,则函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(2)![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(3)![]() 的反函数与
的反函数与![]() 是相同的函数.
是相同的函数.
(4)![]() 无最大值也无最小值.
无最大值也无最小值.
(5)![]() 的最小正周期为
的最小正周期为![]() .
.
(6)![]() 有对称轴两条,对称中心有三个.
有对称轴两条,对称中心有三个.
则正确命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)![]() 是函数
是函数![]() 的极值点,求函数
的极值点,求函数![]() 的单调区间;
的单调区间;
(3)在(2)的条件下,![]() ,若
,若![]() ,
,![]() ,使不等式
,使不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的顶点到直线l1:y=x的距离分别为
(a>b>0)的顶点到直线l1:y=x的距离分别为![]() 和
和![]() .
.
(1)求椭圆C的标准方程
(2)设平行于l1的直线l交C于A,B两点,且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某城市中心花园的边界是圆心为O,直径为1千米的圆,花园一侧有一条直线型公路l,花园中间有一条公路AB(AB是圆O的直径),规划在公路l上选两个点P,Q,并修建两段直线型道路PB,QA.规划要求:道路PB,QA不穿过花园.已知![]() ,
,![]() (CD为垂足),测得OC=0.9,BD=1.2(单位:千米).已知修建道路费用为m元/千米.在规划要求下,修建道路总费用的最小值为_____元.
(CD为垂足),测得OC=0.9,BD=1.2(单位:千米).已知修建道路费用为m元/千米.在规划要求下,修建道路总费用的最小值为_____元.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(1,2)在抛物线C:y2=2px(p>0)上.
(Ⅰ)求C的方程;
(Ⅱ)斜率为﹣1的直线与C交于异于点P的两个不同的点M,N,若直线PM,PN分别与x轴交于A,B两点,求证:△PAB为等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)求购买金额不少于45元的频率;
(2)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
女 | 18 | ||
合计 |
附:参考公式和数据: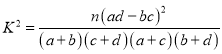 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com