
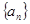 和等比数列
和等比数列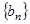 中,
中,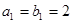 ,
,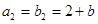 ,
,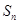 是
是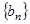 前
前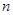 项和.
项和.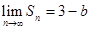 ,求实数
,求实数 的值;
的值; ,使得数列
,使得数列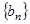 的所有项都在数列
的所有项都在数列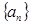 中?若存在,求出所有的
中?若存在,求出所有的 ,若不存在,说明理由;
,若不存在,说明理由; ,使得数列
,使得数列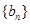 中至少有三项在数列
中至少有三项在数列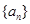 中,但
中,但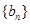 中的项不都在数列
中的项不都在数列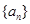 中?若存在,求出一个可能的
中?若存在,求出一个可能的 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.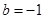 ;(2)存在,
;(2)存在, ;(3)存在,
;(3)存在,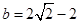 (答案不唯一).
(答案不唯一).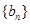 是等比数列,其前
是等比数列,其前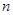 和的极限存在,因此有公式
和的极限存在,因此有公式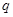 满足
满足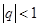 ,且极限为
,且极限为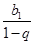 ;(2)由于
;(2)由于 是正整数,因此可对
是正整数,因此可对 按奇偶来分类讨论,因此当
按奇偶来分类讨论,因此当 为奇数时,等比数列
为奇数时,等比数列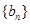 的公比不是整数,是分数,从而数列
的公比不是整数,是分数,从而数列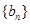 从第三项开始每一项都不是整数,都不在数列
从第三项开始每一项都不是整数,都不在数列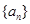 中,而当
中,而当 为偶数时,数列
为偶数时,数列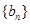 的所有项都在
的所有项都在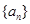 中,设
中,设 ,则
,则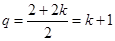 ,
,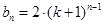 展开有
展开有
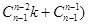
 ,这里用到了二项式定理,
,这里用到了二项式定理,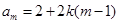 ,结论为真;(3)存在时只要找一个
,结论为真;(3)存在时只要找一个 ,首先
,首先 不能为整数,下面我们只要写两数列的通项公式,让
不能为整数,下面我们只要写两数列的通项公式,让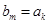
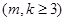 ,取特殊值求出
,取特殊值求出 ,如取
,如取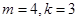 ,可得
,可得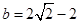 ,此时
,此时 在数列
在数列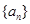 中,由于
中,由于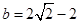 是无理数,会发现数列
是无理数,会发现数列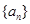 除第一项以外都是无理数,而
除第一项以外都是无理数,而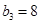 是整数,不在数列
是整数,不在数列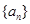 中,命题得证,(如取其它的
中,命题得证,(如取其它的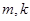 又可得到另外的
又可得到另外的 值).
值).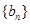 ,公比
,公比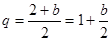 .
.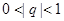 ,所以
,所以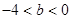 . 2分
. 2分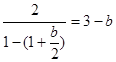 , 4分
, 4分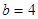 或
或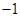 .
. 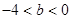 ,所以
,所以 . 6分
. 6分 取偶数
取偶数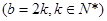 时,
时,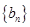 中所有项都是
中所有项都是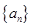 中的项. 8分
中的项. 8分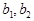 均在数列
均在数列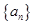 中,
中,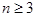 时,
时,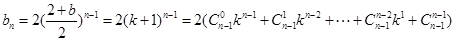
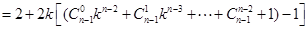
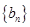 的第n项是
的第n项是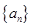 中的第
中的第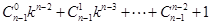 项. 10分
项. 10分 取奇数
取奇数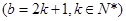 时,因为
时,因为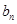 不是整数,
不是整数,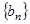 的所有项都不在数列
的所有项都不在数列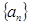 中。 12分
中。 12分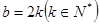 。
。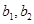 在
在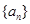 中,所以
中,所以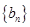 中至少存在一项
中至少存在一项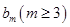 在
在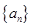 中,另一项
中,另一项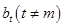 不在
不在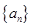 中。 14分
中。 14分 得
得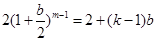 ,
,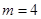 得
得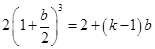 ,即
,即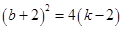 .
.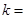 4,得
4,得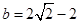 (舍负值)。此时
(舍负值)。此时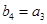 。 16分
。 16分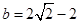 时,
时,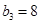 ,
,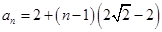 ,对任意
,对任意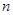 ,
, . 18分
. 18分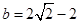 .
.

科目:高中数学 来源:不详 题型:单选题
| A.2100 | B.2600 | C.2800 | D.3100 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①②③ | B.②③ | C.②④ | D.④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
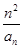 ,证明:bn≤
,证明:bn≤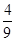 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com