
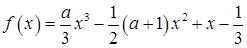 (
(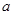
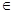 R).
R).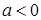 ,求函数
,求函数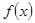 的极值;
的极值;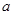 使得函数
使得函数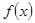 在区间
在区间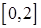 上有两个零点,若存在,求出
上有两个零点,若存在,求出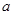 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。 ,
,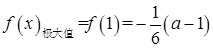 (2)存在实数
(2)存在实数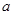 ,当
,当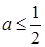 时,函数
时,函数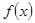 在区间
在区间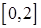 上有两个零点
上有两个零点 ………………2分
………………2分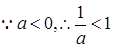 ,
,| | 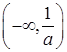 | 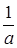 | 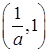 | 1 | 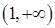 |
 | - | 0 | + | 0 | - |
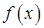 | 递减 | 极小值 | 递增 | 极大值 | 递减 |
 ,
,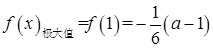 ……6分
……6分 ,
,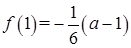
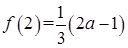 ,
, 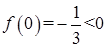 ……………8分
……………8分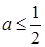 时,
时,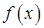 在
在 上为增函数,在
上为增函数,在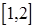 上为减函数,
上为减函数,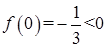 ,
, ,
, ,所以
,所以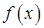 在区间
在区间 ,
, 上各有一个零点,即在
上各有一个零点,即在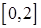 上有两个零点; ………………………10分
上有两个零点; ………………………10分 时,
时,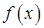 在
在 上为增函数,在
上为增函数,在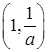 上为减函数,
上为减函数,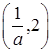 上为增函数,
上为增函数,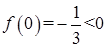 ,
, ,
, ,
,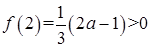 ,所以
,所以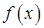 只在区间
只在区间 上有一个零点,故在
上有一个零点,故在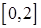 上只有一个零点; ………………………12分
上只有一个零点; ………………………12分 时,
时,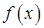 在
在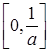 上为增函数,在
上为增函数,在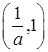 上为减函数,
上为减函数, 上为增函数,
上为增函数,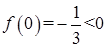 ,
, ,
, ,
,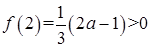 , 所以
, 所以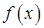 只在区间
只在区间 上有一个零点,故在
上有一个零点,故在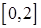 上只有一个零点; …………………………13分
上只有一个零点; …………………………13分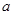 ,当
,当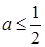 时,函数
时,函数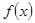 在区间
在区间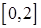 上有两个零点…………………14分
上有两个零点…………………14分

科目:高中数学 来源:不详 题型:单选题
| A.(13,+∞) | B.(5,+∞) | C.(4,+∞) | D.(-∞,13) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
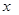 套世博吉祥物“海宝”所需成本费用为
套世博吉祥物“海宝”所需成本费用为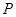 元,且
元,且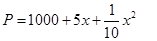 ,而每套“海宝”售出的价格为
,而每套“海宝”售出的价格为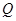 元,其中
元,其中
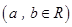 ,
,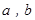 的值.(利润 = 销售收入-成本)
的值.(利润 = 销售收入-成本)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 、
、 之间的“理想距离”为:
之间的“理想距离”为: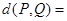
 ;若
;若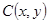 到点
到点 、
、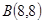 的“理想距离”相等,其中实数
的“理想距离”相等,其中实数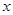 、
、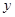 满足
满足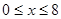 、
、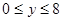 ,则所有满足条件的点
,则所有满足条件的点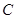 的轨迹的长度之和是
的轨迹的长度之和是A. | B.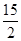 | C.10 | D.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com