
(1)若以l0为一条准线,中心在坐标原点的椭圆恰与直线l也相切,切点为T,求椭圆的方程及点T的坐标;
(2)若直线l与双曲线6x2-λy2=8的两个交点为M、N,且点A为线段MN的中点,又过点E的直线与该双曲线的两支分别交于P、Q两点,记![]() 在x轴正方向上的投影为p,且
在x轴正方向上的投影为p,且![]() p2=m,m∈
p2=m,m∈![]() ,求(1)中切点T到直线PQ的距离的最小值.
,求(1)中切点T到直线PQ的距离的最小值.

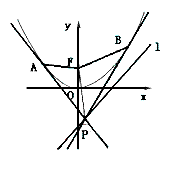
(文)如图,与抛物线x2=-4y相切于点A(-4,-4)的直线l分别交x轴、y轴于点F、E,过点E作y轴的垂线l0.
(1)若以l0为一条准线,中心在坐标原点的椭圆恰好过点F,求椭圆的方程;
(2)若直线l与双曲线6x2-λy2=8的两个交点为M、N,且点A为线段MN的中点,又过点E的直线与该双曲线的两支分别交于P、Q两点,记![]() 在x轴正方向上的投影为p,且
在x轴正方向上的投影为p,且![]() =m,m∈
=m,m∈![]() ,求直线PQ的斜率的取值范围.
,求直线PQ的斜率的取值范围.

(理)解:抛物线x2=-4y中,
∵导数y′=-![]() x,
x,
∴直线l的斜率为y′|x=-4=2.
故直线l的方程为y=2x+4.
∴点F、E的坐标分别为F(-2,0)、E(0,4).
(1)∵直线l0的方程是y=4,
∴以l0为一条准线,中心在坐标原点的椭圆方程可设为![]() =1(a>b>0).则
=1(a>b>0).则![]() =4.
=4.
由 (4b2+a2)x2+16b2x+16b2-a2b2=0.
(4b2+a2)x2+16b2x+16b2-a2b2=0.
∵直线l与椭圆相切,
∴Δ=162b4-4(4b2+a2)(16b2-a2b2)=0.
而![]() =4,a2=b2+c2,
=4,a2=b2+c2,
解得a2=4,b2=3.
∴所求椭圆方程为![]() =1.
=1.
此时,x=![]()
=![]() =-
=-![]() ,
,
即切点T的坐标为T(-![]() ,1).
,1).
(2)设l与双曲线6x2-λy2=8的两个交点为M(x1,y1)、N(x2,y2),显然x1≠x2.
∵点A为线段MN的中点,
∴x1+x2=-8,y1+y2=-8.
由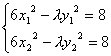
![]()
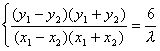 .
.
而kl=![]() =2
=2![]() λ=3.
λ=3.
∴双曲线的方程为6x2-3y2=8,
即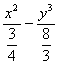 =1.
=1.
∵![]() 在x轴正方向上的投影为p,
在x轴正方向上的投影为p,
∴p2=cos2∠EFO=![]() .
.
设直线PQ的方程为y=kx+4(斜率k必存在),点P(x3,y3),Q(x4,y4).
∴![]() =x3x4+y3y4=
=x3x4+y3y4=![]() =5m.
=5m.
而m∈[![]() ,
,![]() ],
],
∴![]() ≤
≤![]() =x3x4+y3y4≤
=x3x4+y3y4≤![]() .
.
由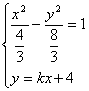
![]() (6-3k2)x2-24kx-56=0.
(6-3k2)x2-24kx-56=0.
∵P、Q两点分别在双曲线的两支上,
∴6-3k2≠0.
∴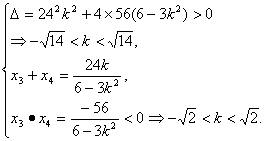
∴-![]() <k<
<k<![]() .
.
此时y3y4=(kx3+4)(kx4+4)=k2x3x4+4k(x3+x4)+16.
∴x3x4+y3y4=(1+k2)x3x4+4k(x3+x4)+16
=![]() (1+k2)+
(1+k2)+![]() +16
+16
=![]()
=![]() .
.
∴![]() ≤
≤![]() ≤
≤![]() .
.
∴40-20k2≤40-8k2
40-8k2≤80-40k2![]() 0≤k2≤
0≤k2≤![]() .
.
又-![]() <k<
<k<![]() ,
,
∴k2∈[0,![]() ],即k∈[-
],即k∈[-![]() ,
,![]() ].
].
而切点T到直线PQ的距离为
d=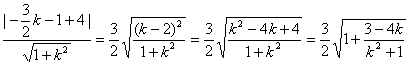 .
.
设t=![]() ,k∈[-
,k∈[-![]() ,
,![]() ],
],
则t′=![]() .
.
令t′>0![]() k<-
k<-![]() 或k>2.
或k>2.
∴t=![]() 在[-
在[-![]() ,-
,-![]() ]上单调递增,在[-
]上单调递增,在[-![]() ,-
,-![]() ]上单调递减.
]上单调递减.
又k=-![]() 时,d=2+
时,d=2+![]() ;k=
;k=![]() 时,d=2-
时,d=2-![]() .
.
∴dmin=2-![]() ,即切点T到直线PQ的距离的最小值为2-
,即切点T到直线PQ的距离的最小值为2-![]() .
.
(文)解:抛物线x2=-4y中,
∵导数y′=-![]() x,
x,
∴直线l的斜率为y′|x=-4=2.
故直线l的方程为y=2x+4.
∴点F、E的坐标分别为F(-2,0)、F(0,4),
(此处也可用Δ=0求切线斜率,再写出方程)
(1)∵直线l0的方程是y=4,
∴以l0为一条准线,经过点F,中心在坐标原点的椭圆方程可设为![]() =1(a>2).
=1(a>2).
则c=![]() ,其准线方程为y=
,其准线方程为y=![]() =
=![]() .
.
由![]() =4,得
=4,得![]() =4,化简得a4=16(a2-4),解得a2=8.
=4,化简得a4=16(a2-4),解得a2=8.
∴椭圆方程为![]() =1.
=1.
(2)设l与双曲线6x2-λy2=8的两个交点为M(x1,y1)、N(x2,y2),显然x1≠x2.
∵点A为线段MN的中点,
∴x1+x2=-8,y1+y2=-8.
由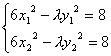
![]()
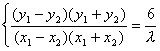 .
.
∵kl=![]() =2
=2![]() λ=3.
λ=3.
∴双曲线的方程为6x2-3y2=8,
即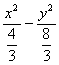 =1.
=1.
∵![]() 在x轴正方向上的投影为p,
在x轴正方向上的投影为p,
∴p2=cos2∠EFO=![]() .
.
设直线PQ的方程为y=kx+4(斜率k必存在),点P(x3,y3),Q(x4,y4).
∴![]() =x3x4+y3y4=
=x3x4+y3y4=![]() =5m.
=5m.
而m∈[![]() ,
,![]() ],
],
∴![]() ≤
≤![]() =x3x4+y3y4≤
=x3x4+y3y4≤![]() .
.
由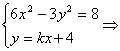 (6-3k2)x2-24kx-56=0.
(6-3k2)x2-24kx-56=0.
∵P、Q两点分别在双曲线的两支上,
∴6-3k2≠0.
∴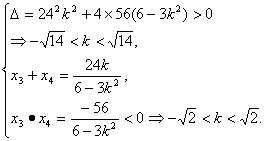
∴-![]() <k<
<k<![]() .
.
此时y3y4=(kx3+4)(kx4+4)=k2x3x4+4k(x3+x4)+16.
∴x3x4+y3y4=(1+k2)x3x4+4k(x3+x4)+16
=![]() (1+k2)+
(1+k2)+![]() +16
+16
=![]() =
=![]() .
.
∴![]() ≤
≤![]() ≤
≤![]() .
.
∴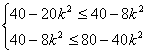
![]() 0≤k2≤
0≤k2≤![]() .
.
又-![]() <k<
<k<![]() ,∴k2∈[0,
,∴k2∈[0, ![]() ].
].
∴k∈[![]() ,
,![]() ].
].
故所求直线PQ的斜率的取值范围是[![]() ,
,![]() ].
].


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(07年安徽卷理)如图,抛物线y=-x2+1与x轴的正半轴交于点A,将线段OA的n等分点从左至右依次记为P1,P2,…,Pn-1,过这些分点分别作x轴的垂线,与抛物线的交点依次为Q1,Q2,…,Qn-1,从而得到n-1个直角三角形△Q1OP1, △Q2P1P2,…, △Qn-1Pn-1Pn-1,当n→∞时,这些三角形的面积之和的极限为 .

查看答案和解析>>
科目:高中数学 来源: 题型:
(05年江西卷理)(14分)
如图,设抛物线![]() 的焦点为F,动点P在直线
的焦点为F,动点P在直线![]() 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
(1)求△APB的重心G的轨迹方程.
(2)证明∠PFA=∠PFB.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年黄冈中学三模理)如图,设抛物线![]()
![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,焦点为
,焦点为![]() ;以
;以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆
的椭圆![]() 与抛物线
与抛物线![]() 在
在![]() 轴上方的一个交点为
轴上方的一个交点为![]() .
.
(Ⅰ)当![]() 时,求椭圆的方程及其右准线的方程;
时,求椭圆的方程及其右准线的方程;
(Ⅱ)在(Ⅰ)的条件下,直线![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() ,如果
,如果
以线段![]() 为直径作圆,试判断点P与圆的位置关系,并说明理由;
为直径作圆,试判断点P与圆的位置关系,并说明理由;
(Ⅲ)是否存在实数![]() ,使得△
,使得△![]() 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
(04年北京卷理)(14分)
如图,过抛物线y2=2px (p>0) 上一定点P(x0, y0) (y0>0),作两条直线分别交抛物线于A(x1,y1),B(x2,y2).
(I)求该抛物线上纵坐标为![]() 的点到其焦点F的距离;
的点到其焦点F的距离;
(II)当PA与PB的斜率存在且倾斜角互补时,
求![]() 的值,并证明直线AB的斜率是非零常数。
的值,并证明直线AB的斜率是非零常数。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com