
分析 (Ⅰ)根据函数解析式计算f(-$\frac{π}{6}$)即可;
(Ⅱ)化f(x)为sinx的二次函数,利用三角函数的有界性和二次函数的性质求出f(x)的最值即可.
解答 解:函数f(x)=cos2x+2sinx,
(Ⅰ)f(-$\frac{π}{6}$)=cos(-$\frac{π}{3}$)+2sin(-$\frac{π}{6}$)
=$\frac{1}{2}$+2×(-$\frac{1}{2}$)
=-$\frac{1}{2}$;
(Ⅱ)f(x)=(1-2sin2x)+2sinx=-2${(sinx-\frac{1}{2})}^{2}$+$\frac{3}{2}$,
∴当x=$\frac{π}{6}$+2kπ或x=$\frac{5π}{6}$+2kπ,k∈Z时,f(x)取得最大值$\frac{3}{2}$;
当x=-$\frac{π}{2}$+2kπ,k∈Z时,f(x)取得最小值-3;
∴f(x)的值域是[-3,$\frac{3}{2}$].
点评 本题考查了三角函数求值的应用问题,也考查了二次函数的性质与应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
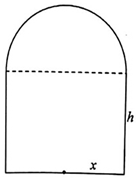 某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
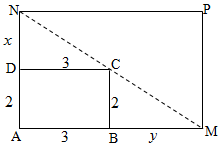 如图,矩形草坪AMPN中,点C在对角线MN上.CD垂直于AN于点D,CB垂直于AM于点B,|CD|=|AB|=3米,|AD|=|BC|=2米,设|DN|=x米,|BM|=y米.求这块矩形草坪AMPN面积的最小值.
如图,矩形草坪AMPN中,点C在对角线MN上.CD垂直于AN于点D,CB垂直于AM于点B,|CD|=|AB|=3米,|AD|=|BC|=2米,设|DN|=x米,|BM|=y米.求这块矩形草坪AMPN面积的最小值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,7) | B. | (7,7) | C. | (7,1) | D. | (3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{7}{5}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
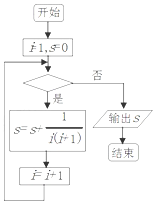 一个算法的框图如右图所示,若该程序输出的结果为$\frac{5}{6}$,则判断框中应填入的条件是( )
一个算法的框图如右图所示,若该程序输出的结果为$\frac{5}{6}$,则判断框中应填入的条件是( )| A. | i<6 | B. | i≤6 | C. | i<5 | D. | i≤7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com