
【题目】某种商品在天![]() 内每克的销售价格
内每克的销售价格![]() (元)与时间
(元)与时间![]() 的函数图象是如图所示的两条线段
的函数图象是如图所示的两条线段![]() (不包含
(不包含![]() 两点);该商品在 30 天内日销售量
两点);该商品在 30 天内日销售量![]() (克)与时间
(克)与时间![]() (天)之间的函数关系如下表所示:
(天)之间的函数关系如下表所示:
第 | 5 | 15 | 20 | 30 |
销售量 | 35 | 25 | 20 | 10 |

(1)根据提供的图象,写出该商品每克销售的价格![]() (元)与时间
(元)与时间![]() 的函数关系式;
的函数关系式;
(2)根据表中数据写出一个反映日销售量![]() 随时间
随时间![]() 变化的函数关系式;
变化的函数关系式;
(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的![]() 值.
值.
(注:日销售金额=每克的销售价格×日销售量)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)25.
;(3)25.
【解析】
(1)设AB所在的直线方程为P=kt+20,将B点代入可得k值,由CD两点坐标可得直线CD所在的两点式方程,进而可得销售价格P(元)与时间t的分段函数关系式.
(2)设Q=k1t+b,把两点(5,35),(15,25)的坐标代入,可得日销售量Q随时间t变化的函数的解析式
(3)设日销售金额为y,根据销售金额=销售价格×日销售量,结合(1)(2)的结论得到答案.
(1)由图可知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() 所在直线方程为
所在直线方程为![]() ,把
,把![]() 代入
代入![]()
得![]() ,所以.
,所以. ![]() ,
,
由两点式得![]() 所在的直线方程为
所在的直线方程为![]() ,
,
整理得,![]() ,
,![]() ,所以
,所以![]() ,
,
(2)由题意,设![]() ,把两点
,把两点![]() ,
,![]() 代入得
代入得![]() ,
,
解得![]() 所以
所以![]()
把点![]() ,
,![]() 代入
代入![]() 也适合,即对应的四点都在同一条直线上,
也适合,即对应的四点都在同一条直线上,
所以![]() .
.
(本题若把四点中的任意两点代入![]() 中求出
中求出![]() ,
,![]() ,再验证也可以)
,再验证也可以)
(3)设日销售金额为![]() ,依题意得,
,依题意得,
当![]() 时
时![]() ,配方整理得
,配方整理得![]() ,
,
当![]() 时,
时,![]() 在区间
在区间![]() 上的最大值为900
上的最大值为900
当![]() 时,
时,![]() ,配方整理得
,配方整理得![]() ,
,
所以当![]() 时,
时,![]() 在区间上的最大值为1125.
在区间上的最大值为1125.
综上可知日销售金额最大值为1125元,此时![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函数f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
② 求函数g(x)在x∈[0,2]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将两块三角板按图甲方式拼好,其中![]() ,
, ![]() ,
, ![]() ,
,
![]() ,现将三角板
,现将三角板![]() 沿
沿![]() 折起,使
折起,使![]() 在平面
在平面![]() 上的射影
上的射影![]() 恰好在
恰好在![]() 上,如图乙.
上,如图乙.
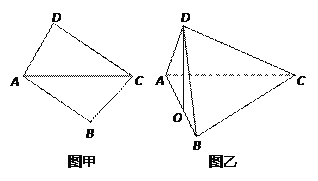
(1)求证: ![]() ;
;
(2)求证: ![]() 为线段
为线段![]() 中点;
中点;
(3)求二面角![]() 的大小的正弦值.
的大小的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】锐角△ABC中,角A,B,C所对的边分别为a,b,c,且acosB+bcosA= ![]() csinC.
csinC.
(1)求cosC;
(2)若a=6,b=8,求边c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sinx,﹣1),
sinx,﹣1), ![]() =(cosx,m),m∈R.
=(cosx,m),m∈R.
(1)若m= ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)已知函数f(x)=2( ![]() +
+ ![]() )
) ![]() ﹣2m2﹣1,若函数f(x)在[0,
﹣2m2﹣1,若函数f(x)在[0, ![]() ]上有零点,求m的取值范围.
]上有零点,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在非零实数
,若存在非零实数![]() 满足对任意
满足对任意![]() ,均有
,均有![]() ,且
,且![]() ,则称
,则称![]() 为
为![]() 上的
上的![]() 高调函数. 如果定义域为
高调函数. 如果定义域为![]() 的函数
的函数![]() 是奇函数,当
是奇函数,当![]() 时,
时,![]() ,且
,且![]() 为
为![]() 上的8高调函数,那么实数
上的8高调函数,那么实数![]() 的取值范围为____.
的取值范围为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校的![]() 名男生中随机抽取
名男生中随机抽取![]() 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,第八组
,第八组![]() ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为![]() 人。
人。

(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的![]() 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为![]() ,事件
,事件![]() ,事件
,事件![]() ,求
,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个不相等的非零向量 ![]() ,
, ![]() ,两组向量
,两组向量 ![]() 和
和 ![]() 均由2个
均由2个 ![]() 和3个
和3个 ![]() 排列而成,记S=
排列而成,记S= ![]() ,Smin表示S所有可能取值中的最小值,则下列命题中
,Smin表示S所有可能取值中的最小值,则下列命题中
1)S有5个不同的值;(2)若 ![]() ⊥
⊥ ![]() 则Smin与|
则Smin与| ![]() |无关;(3)若
|无关;(3)若 ![]() ∥
∥ ![]() 则Smin与|
则Smin与| ![]() |无关;(4)若|
|无关;(4)若| ![]() |>4|
|>4| ![]() |,则Smin>0;(5)若|
|,则Smin>0;(5)若| ![]() |=2|
|=2| ![]() |,Smin=8|
|,Smin=8| ![]() |2 , 则
|2 , 则 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() .正确的是( )
.正确的是( )
A.(1)(2)
B.(2)(4)
C.(3)(5)
D.(1)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com