
 是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的
是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的 是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的什么条件,主要是考查由谁推出谁的问题.先由等轴双曲线方程求出三参数a,b,c;据离心率
是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的什么条件,主要是考查由谁推出谁的问题.先由等轴双曲线方程求出三参数a,b,c;据离心率 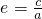 求出离心率,再考查反过来成立与否.
求出离心率,再考查反过来成立与否.
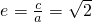 ,
, ,
, 是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的必要条件;
是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的必要条件; 也能得到实轴长与虚轴长相等,
也能得到实轴长与虚轴长相等, 是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的充分条件.
是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的充分条件. 是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的充要条件.
是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的充要条件.

科目:高中数学 来源: 题型:
| ||
| 2 |
| x2 |
| 3 |
| 1 |
| 2 |
4
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
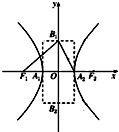 我们把离心率为e=
我们把离心率为e=
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2y2 | ||
|
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知双曲线![]() -
-![]() =1的离心率e>1+
=1的离心率e>1+![]() ,左、右焦点分别为F1,F2,左准线为l,能否在双曲线的左支上找到一点P,使得|PF1|是P到l的距离d与|PF2|的等比中项?
,左、右焦点分别为F1,F2,左准线为l,能否在双曲线的左支上找到一点P,使得|PF1|是P到l的距离d与|PF2|的等比中项?
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省深圳市龙岗区高二(上)期末数学试卷(文科)(解析版) 题型:选择题
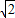 是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的( )
是双曲线为等轴双曲线(实轴长与虚轴长相等的双曲线)的( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com