
【题目】袋中装有除颜色外形状大小完全相同的6个小球,其中有4个编号为1,2, 3, 4的红球,2个编号为A、B的黑球,现从中任取2个小球.;
(1)求所取2个小球都是红球的概率;
(2)求所取的2个小球颜色不相同的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)利用列举法求出任取2个小球的基本事件总数,用![]() 表示“所取取2个小球都是红球”,利用列举法求出
表示“所取取2个小球都是红球”,利用列举法求出![]() 包含的基本事件个数,由此能求出所取取2个小球都是红球的概率.
包含的基本事件个数,由此能求出所取取2个小球都是红球的概率.
(2)用![]() 表示“所取的2个小球颜色不相同”,利用列举法求出
表示“所取的2个小球颜色不相同”,利用列举法求出![]() 包含的基本事件个数,由此能求出所取的2个小球颜色不相同的概率.
包含的基本事件个数,由此能求出所取的2个小球颜色不相同的概率.
(1)由题意知,任取2个小球的基本事件有:
{1,2},{1,3},{1,4},{1,A},{1,B},{2,3},{2,4},{2,A},
{2,B},{3,4},{3,A},{3,B},{4,A},{4,B},{A,B},共15个,
用M表示“所取取2个小球都是红球”,
则M包含的基本事件有:
{1,2},{1,4},{2,3},{2,4},{3,4},共6个,
∴所取取2个小球都是红球的概率:P(M)![]() .
.
(2)用N表示“所取的2个小球颜色不相同”,
则N包含的基本事件有:
{1,A},{1,B},{2,A},{2,B},{3,A},{3,B},{4,A},{4,B},共8个,
∴所取的2个小球颜色不相同的概率:P(N)![]() .
.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
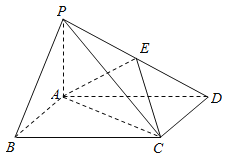
(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 图象在
图象在![]() 处的切线方程;
处的切线方程;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() 存在极大值和极小值,且极大值小于极小值,求
存在极大值和极小值,且极大值小于极小值,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一布袋中装有![]() 个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
A. 若![]() ,则乙有必赢的策略B. 若
,则乙有必赢的策略B. 若![]() ,则甲有必赢的策略
,则甲有必赢的策略
C. 若![]() ,则甲有必赢的策略D. 若
,则甲有必赢的策略D. 若![]() ,则乙有必赢的策略
,则乙有必赢的策略
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,过点
,过点![]() 作直线
作直线![]() 与抛物线
与抛物线![]() 交于不同两点
交于不同两点![]() 、
、![]() ,过
,过![]() 作
作![]() 轴的垂线分别与直线
轴的垂线分别与直线![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求抛物线![]() 的方程;
的方程;
(2)写出抛物线的焦点坐标和准线方程;
(3)求证:![]() 为线段
为线段![]() 的中点.
的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:
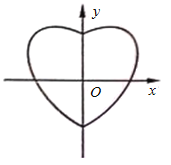
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过![]() ;
;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com