练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知点P是抛物线y2=2x上的动点，点P到准线的距离为d，且点P在y轴上的射影是M，点A（$\frac{7}{2}$，4），则|PA|+|PM|的最小值是（　　）
    A．$\frac{7}{2}$B．4C．$\frac{9}{2}$D．5

    分析 利用抛物线的定义，推出当A、P、M共线时，|PA|+|PM|取得最小值，由此求得答案．

    解答 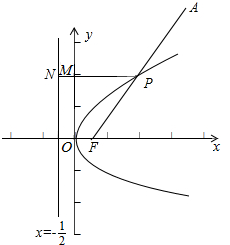解：抛物线焦点F（$\frac{1}{2}$，0），准线x=-$\frac{1}{2}$，延长PM交准线于N，由抛物线定义|PF|=|PN|，
    ∵|PA|+|PM|+|MN|=|PA|+|PN|=|PA|+|PF|≥|AF|=5，而|MN|=$\frac{1}{2}$，∴PA|+|PM|≥5-$\frac{1}{2}$=$\frac{9}{2}$，
    当且仅当A，P，F三点共线时，取“=”号，此时，P位于抛物线上，∴|PA|+|PM|的最小值为：$\frac{9}{2}$，
    故选：C．

    点评 本题主要考查抛物线的定义、标准方程，以及简单性质的应用，体现了数形结合的数学思想，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    15．函数f（x）=$\sqrt{{3}^{x}-1}$+logx（4-3x）的定义域用区间表示为（0，1）∪（1，$\frac{4}{3}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．有10件产品，其中有2件次品，每次抽取1件检验，抽检后不放回，共抽2次，则第1次抽到正品，第2次抽到次品的概率是（　　）
    A．$\frac{32}{45}$B．$\frac{16}{45}$C．$\frac{8}{45}$D．$\frac{4}{45}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．计算tan$\frac{π}{8}-\frac{1}{{tan\frac{π}{8}}}$=-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知锐角α，β满足：sinβ=3cos（α+β）sinα，且α+β≠$\frac{π}{2}$
    （Ⅰ）求证：tan（α+β）=4tanα；
    （Ⅱ）求tanβ的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设集合P={x|y=log2x}，Q={y|y=x2+1}，则P∩Q=（　　）
    A．（1，+∞）B．[0，+∞）C．（0，+∞）D．[1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知a=log510，b=log36，c=log714，则a，b，c按照由小到大的顺序排列为c＜a＜b．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数f（x）=$\frac{x}{3x+1}$，数列{an}满足a1=1，an+1=f（an）（n∈N*），求证：数列{$\frac{1}{{a}_{n}}$}是等差数列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知x，y∈R+，$\frac{1}{x}$+$\frac{1}{y}$=1，求$\frac{4}{x-1}$+$\frac{9}{y-1}$的最值．

    查看答案和解析>>

    同步练习册答案