练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

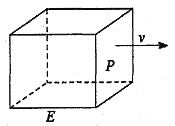
    【题目】如图，长方形物体E在雨中沿面P（面积为S）的垂直方向作匀速移动，速度为，雨速沿E移动方向的分速度为。E移动时单位时间内的淋雨量包括两部分：（1）P或P的平行面（只有一个面淋雨）的淋雨量，假设其值与×S成正比，比例系数为；（2）其它面的淋雨量之和，其值为，记为E移动过程中的总淋雨量，当移动距离d=100，面积S=时。

    （1）写出的表达式

    （2）设0＜v≤10,0＜c≤5，试根据c的不同取值范围，确定移动速度，使总淋雨量最少。

    【答案】（1）

    （2）当时，

    【解析】（1）由题意知，E移动时单位时间内的淋雨量为，

    故.

    （2）由（1）知，当时，

    当时，

    故。

    (1)当时， 是关于的减函数.故当时， 。

    (2) 当时，在上， 是关于的减函数；在上， 是关于的增函数；故当时， 。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝loga(1＋x)，g(x)＝loga(1－x)，(a>0，a≠1).

    (1)设a＝2，函数f(x)的定义域为[3，63]，求f(x)的最值；

    (2)求使f(x)－g(x)>0的x的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

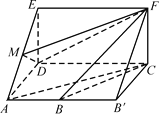
    【题目】如图，四边形ABCD是梯形，四边形CDEF是矩形，且平面ABCD⊥平面CDEF，∠BAD＝∠CDA＝90°，，M是线段AE上的动点．

    （1）试确定点M的位置，使AC∥平面MDF，并说明理由；

    （2）在（1）的条件下，求平面MDF将几何体ADE－BCF分成的两部分的体积之比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中， 平面， ， ， ， 为上一点， 平面．

    （Ⅰ）证明： 平面；

    （Ⅱ）若，求四棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆： 过椭圆： ()的短轴端点， ， 分别是圆与椭圆上任意两点，且线段长度的最大值为3．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）过点作圆的一条切线交椭圆于， 两点，求的面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数， ．

    （Ⅰ）讨论的极值点的个数；

    （Ⅱ）若对于任意，总有成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f(x)的最小值为1，且f(0)＝f(2)＝3.

    (1)求f(x)的解析式；

    (2)若f(x)在区间[2a，a＋1]上不单调，求实数a的取值范围；

    (3)在区间[－1,1]上，y＝f(x)的图象恒在y＝2x＋2m＋1的图象上方，试确定实数m的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥的底面为矩形，D为

    的中点，AC⊥平面BCC1B1．

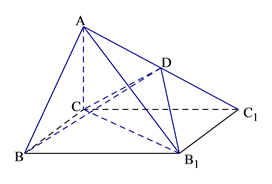
    （Ⅰ）证明：AB//平面CDB1;

    （Ⅱ）若AC=BC=1，BB1=,

    （1）求BD的长；

    （2）求三棱锥C-DB1C1的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以直角坐标系的原点为极点， 轴的正半轴为极轴，并在两种坐标系中取相同的长度单位，点的极坐标为，圆以为圆心，4为半径；又直线的极坐标方程为。

    （Ⅰ）求直线和圆的普通方程；

    （Ⅱ）试判定直线和圆的位置关系．若相交，则求直线被圆截得的弦长．

    查看答案和解析>>

    同步练习册答案