
【题目】观察以下5个等式:
-1=-1
-1+3=2
-1+3-5=-3
-1+3-5+7=4
-1+3-5+7-9=-5
……
根据以上式子规律:
(1)写出第6个等式,并猜想第n个等式;(n∈N*)
(2)用数学归纳法证明上述所猜想的第n个等式成立.(n∈N*)
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)先写出第六个等式,再用归纳推理猜想出结论;(2)借助题设条件运用数学归纳法求解.
试题解析:
(1)第6个等式为-1+3-5+7-9+11=6
第n个等式为 -1+3-5+7-9+……+(-1)n(2n-1)=(-1)nn
(2)下面用数学归纳法给予证明:
-1+3-5+7-9+……+![]() (2n-1)=
(2n-1)=![]() n
n
(1)当![]() 时,由已知得原式成立;
时,由已知得原式成立;
(2)假设当![]() 时,原式成立,
时,原式成立,
即-1+3-5+7-9+……+(-1)k (2k-1)=(-1)kk
那么,当![]() 时,
时,
-1+3-5+7-9+……+![]() (2k-1)+
(2k-1)+![]() (2k+1)=
(2k+1)=![]() k+
k+![]() (2k+1)
(2k+1)
=![]() (-k+2k+1)
(-k+2k+1)
=(-1)k+1 (k+1)
故当![]() 时,原式也成立.
时,原式也成立.
由(1)(2)可知:-1+3-5+7-9+……+![]() (2n-1)=
(2n-1)=![]() n对n∈N*都成立。
n对n∈N*都成立。


科目:高中数学 来源: 题型:
【题目】现从80瓶水中抽取6瓶进行检验,利用随机数表抽取样本时,先将80瓶水编号,可以编为00,01,02,……,79,在随机数表中任选一个数,例如选出第6行第5列的数7(下面摘取了附表1的第6行至第10行)。
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
57 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28
规定从选定的数7开始向右读, 依次得到的样本为__________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切正整数
,对一切正整数![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上,记
的图象上,记![]() 与
与![]() 的等差中项为
的等差中项为![]() 。
。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)设集合![]() ,等差数列
,等差数列![]() 的任意一项
的任意一项![]() ,其中
,其中![]() 是
是![]() 中的最小数,且
中的最小数,且![]() ,求
,求![]() 的通项公式。
的通项公式。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,把两个全等的![]() 和
和![]() 分别置于平面直角坐标系中,使直角边
分别置于平面直角坐标系中,使直角边![]() 在
在![]() 轴上,已知点
轴上,已知点![]() ,过
,过![]() 两点的直线分别交
两点的直线分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() . 抛物线
. 抛物线![]() 经过
经过![]() 三点.
三点.
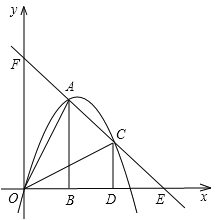
(1)求该抛物线的函数解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的平行线交抛物线于点
轴的平行线交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,问是否存在这样的点
,问是否存在这样的点![]() ,使得四边形
,使得四边形![]() 为等腰梯形?若存在,求出此时点
为等腰梯形?若存在,求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若![]() 沿
沿![]() 方向平移(点
方向平移(点![]() 始终在线段
始终在线段![]() 上,且不与点
上,且不与点![]() 重合),
重合),![]() 在平移的过程中与
在平移的过程中与![]() 重叠部分的面积记为
重叠部分的面积记为![]() ,试探究
,试探究![]() 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<![]() )为多大时,水渠中水的流失量最小?
)为多大时,水渠中水的流失量最小?
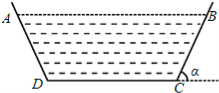
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2016 年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元(
万元(![]() )满足
)满足![]() 为常数),如果不搞促销活动,则该产品的年销售只能是
为常数),如果不搞促销活动,则该产品的年销售只能是![]() 万件.已知2016 年生产该产品的固定投入为
万件.已知2016 年生产该产品的固定投入为![]() 万元.每生产
万元.每生产![]() 万件该产品需要再投入
万件该产品需要再投入![]() 万元,厂家将每件产品的销售价格定为每件产品年平均成本的
万元,厂家将每件产品的销售价格定为每件产品年平均成本的![]() 倍(产品成本包括固定投入和再投入两部分资金).
倍(产品成本包括固定投入和再投入两部分资金).
(1)将2016 年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2016 年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】尧盛机械生产厂每生产某产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为
(万元),其中固定成本为![]() 万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入
万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入![]() (万元)满足
(万元)满足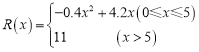 ,假定生产的产品都能卖掉,请完成下列问题:
,假定生产的产品都能卖掉,请完成下列问题:
(1)写出利润函数![]() 的解析式(注:利润=销售收入-总成本);
的解析式(注:利润=销售收入-总成本);
(2)试问该工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com