
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为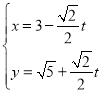 (
(![]() 为参数)。在极坐标系(与直角坐标系
为参数)。在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 。
。
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人各进行![]() 次射击,甲每次击中目标的概率为
次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率
,乙每次击中目标的概率![]() ,
,
(Ⅰ)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望;
的概率分布及数学期望;
(Ⅱ)求甲恰好比乙多击中目标![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. “![]() ”是“
”是“![]() ”成立的充分不必要条件
”成立的充分不必要条件
B. 命题![]() ,则
,则![]()
C. 为了了解800名学生对学校某项教改试验的意见,用系统抽样的方法从中抽取一个容量为40的样本,则分组的组距为40
D. 已知回归直线的斜率的估计值为1.23,样本点的中心为![]() ,则回归直线方程为
,则回归直线方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司投资开发某种新能源产品,估计能获得10万元到100万元的投资收益,现准备制定一个对科研课题组的奖励方案:①奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加;②奖金不超过9万元;③奖金不超过投资收益的20%.
(单位:万元)的增加而增加;②奖金不超过9万元;③奖金不超过投资收益的20%.
(1)若建立函数![]() 模型制定奖励方案,试用数学语言表述该公司对奖励函数
模型制定奖励方案,试用数学语言表述该公司对奖励函数![]() 模型的基本要求,并分析函数
模型的基本要求,并分析函数![]() 是否符合公司要求的奖励函数模型,并说明原因;
是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用模型函数![]() 作为奖励函数模型,试确定最小的正整数
作为奖励函数模型,试确定最小的正整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com