
设椭圆E:  (a,b>0)过M(2,
(a,b>0)过M(2, ) ,N(
) ,N( ,1)两点,O为坐标原点,(I)求椭圆E的方程;
,1)两点,O为坐标原点,(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
(1)因为椭圆E: 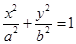 (a,b>0)过M(2,
(a,b>0)过M(2,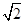 ) ,N(
) ,N(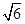 ,1)两点,
,1)两点,
所以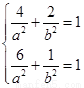 解得
解得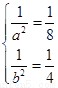 所以
所以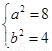 椭圆E的方程为
椭圆E的方程为 …………5分
…………5分
(2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且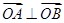 ,设该圆的切线方程为
,设该圆的切线方程为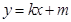 解方程组
解方程组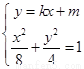 得
得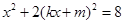 ,即
,即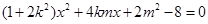 ,
,
则△=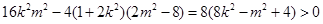 ,即
,即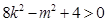
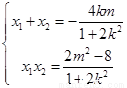
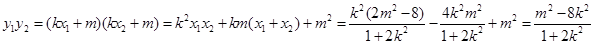 要使
要使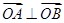 ,需使
,需使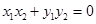 ,即
,即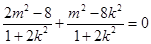 ,所以
,所以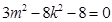 ,所以
,所以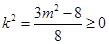 又
又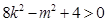 ,所以
,所以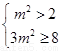 ,所以
,所以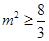 ,即
,即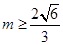 或
或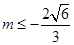 ,因为直线
,因为直线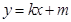 为圆心在原点的圆的一条切线,所以圆的半径为
为圆心在原点的圆的一条切线,所以圆的半径为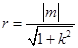 ,
,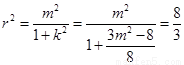 ,
,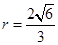 ,所求的圆为
,所求的圆为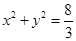 ,此时圆的切线
,此时圆的切线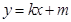 都满足
都满足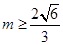 或
或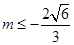 ,而当切线的斜率不存在时切线为
,而当切线的斜率不存在时切线为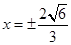 与椭圆
与椭圆 的两个交点为
的两个交点为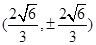 或
或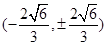 满足
满足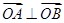 ,综上, 存在圆心在原点的圆
,综上, 存在圆心在原点的圆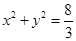 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且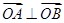 .
.
因为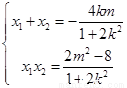 ,
,
所以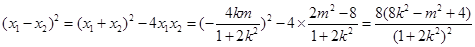 ,
,
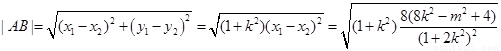
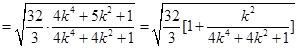 ,
,
①当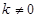 时
时
因为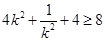 所以
所以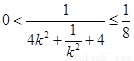 ,
,
所以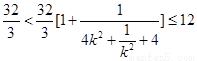 ,
,
所以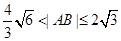 当且仅当
当且仅当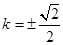 时取”=”.
时取”=”.
② 当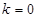 时,
时,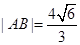 .
.
③ 当AB的斜率不存在时, 两个交点为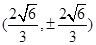 或
或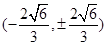 ,所以此时
,所以此时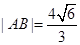 ,
,
综上, |AB |的取值范围为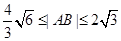 即:
即:
【解析】略


科目:高中数学 来源: 题型:
设椭圆E: ![]() (a,b>0)过M(2,
(a,b>0)过M(2,![]() ) ,N(
) ,N(![]() ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且![]() ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009山东卷理) (本小题满分14分)
设椭圆E: ![]() (a,b>0)过M(2,
(a,b>0)过M(2,![]() ) ,N (
) ,N (![]() ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且![]() ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
查看答案和解析>>
科目:高中数学 来源:2014届河南省高二上学期期末考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)
设椭圆E: 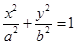 (a,b>0)过M(2,
(a,b>0)过M(2,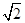 ) ,N(
) ,N(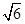 ,1)两点,O为坐标原点.
,1)两点,O为坐标原点.
(Ⅰ)求椭圆E的方程;
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交A,B且
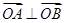 ?若存在,写出该圆的方程,若不存在说明理由。
?若存在,写出该圆的方程,若不存在说明理由。
|
查看答案和解析>>
科目:高中数学 来源:2012届河北省高三下学期理科数学试卷 题型:解答题
设椭圆E:  (a,b>0)过M(2,
(a,b>0)过M(2, )
,N(
)
,N(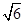 ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且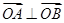 ?若存在,写出该圆的方程,并求|AB|的取值范围,若不存在说明理由
?若存在,写出该圆的方程,并求|AB|的取值范围,若不存在说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com