
【题目】已知m∈R,命题p:对任意x∈[0,1],不等式x2﹣2x﹣1≥m2﹣3m恒成立,命题q:存在x∈[﹣1,1],使得m≤2x﹣1;
(Ⅰ)若命题p为真命题,求m的取值范围;
(Ⅱ)若命題q为假命题,求m的取值范围.
科目:高中数学 来源: 题型:
【题目】从某工厂的一个车间抽取某种产品![]() 件,产品尺寸(单位:
件,产品尺寸(单位:![]() )落在各个小组的频数分布如下表:
)落在各个小组的频数分布如下表:
数据分组 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)根据频数分布表,求该产品尺寸落在![]() 的概率;
的概率;
(2)求这![]() 件产品尺寸的样本平均数
件产品尺寸的样本平均数![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经过计算得
,经过计算得![]() ,利用该正态分布,求
,利用该正态分布,求![]() .
.
附:①若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在极坐标系中,点![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点,以极点为原点,极轴为
的中点,以极点为原点,极轴为![]() 轴的正半轴,并在两坐标系中取相同的长度单位,建立平面直角坐标系,曲线
轴的正半轴,并在两坐标系中取相同的长度单位,建立平面直角坐标系,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 过点
过点![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知梯形![]() 如图(1)所示,其中
如图(1)所示,其中![]() ,
, ![]() ,四边形
,四边形![]() 是边长为
是边长为![]() 的正方形,现沿
的正方形,现沿![]() 进行折叠,使得平面
进行折叠,使得平面![]() 平面
平面![]() ,得到如图(2)所示的几何体.
,得到如图(2)所示的几何体.
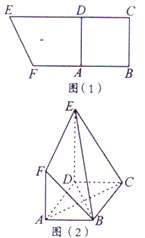
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知点![]() 在线段
在线段![]() 上,且
上,且![]() 平面
平面![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在![]() .
.
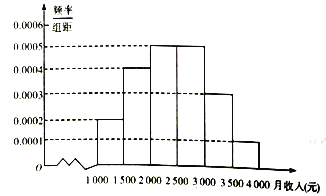
(1)求居民收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数、平均数及其众数;
(3)为了分析居民的收入与年龄、职业等方面的关系,从这10000人中用分层抽样方法抽出100人作进一步分析,则应月收入为![]() 的人中抽取多少人?
的人中抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数g(x)=ax2+c(a,c∈R),g(1)=1且不等式g(x)≤x2﹣x+1对一切实数x恒成立.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)在(Ⅰ)的条件下,设函数h(x)=2g(x)﹣2,关于x的不等式h(x﹣1)+4h(m)≤h(![]() )﹣4m2h(x),在x∈[
)﹣4m2h(x),在x∈[![]() ,+∞)有解,求实数m的取值范围.
,+∞)有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2-(2m+1)x+m.
(1)若方程f(x)=0有两个不等的实根x1,x2,且-1<x1<0<x2<1,求m的取值范围;
(2)若对任意的x∈[1,2],![]() ≤2恒成立,求m的取值范围.
≤2恒成立,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com