
【题目】如图所示的折线图为某小区小型超市今年1月份到5月份的营业额和支出数据(利润=营业额-支出),根据折线图,下列说法正确的是( )

A.该超市这五个月中的营业额一直在增长;
B.该超市这五个月的利润一直在增长;
C.该超市这五个月中五月份的利润最高;
D.该超市这五个月中的营业额和支出呈正相关.
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市移动公司为了提高服务质量,决定对使用A,B两种套餐的集团用户进行调查,准备从本市![]() 个人数超过1000人的大集团和8个人数低于200人的小集团中随机抽取若干个集团进行调查,若一次抽取2个集团,全是小集团的概率为
个人数超过1000人的大集团和8个人数低于200人的小集团中随机抽取若干个集团进行调查,若一次抽取2个集团,全是小集团的概率为![]() .
.
![]() 求n的值;
求n的值;
![]() 若取出的2个集团是同一类集团,求全为大集团的概率;
若取出的2个集团是同一类集团,求全为大集团的概率;
![]() 若一次抽取4个集团,假设取出小集团的个数为X,求X的分布列和期望.
若一次抽取4个集团,假设取出小集团的个数为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为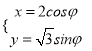 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求经过椭圆![]() 右焦点
右焦点![]() 且与直线
且与直线![]() 垂直的直线的极坐标方程;
垂直的直线的极坐标方程;
(2)若![]() 为椭圆
为椭圆![]() 上任意-点,当点
上任意-点,当点![]() 到直线
到直线![]() 距离最小时,求点
距离最小时,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众,调查结果如下面的2×2列联表.
“非体育迷” | “体育迷” | 总计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
总计 | 75 | 25 | 100 |
(1)据此资料判断是否有90%的把握认为“体育迷”与性别有关.
(2)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”共有5人,其中女性2名,男性3名,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周上有![]() 个白点,先将其中一个染为黑色(称为第一次染色),对任何正整数
个白点,先将其中一个染为黑色(称为第一次染色),对任何正整数![]() ,第
,第![]() 次染色后按逆时针方向间隔
次染色后按逆时针方向间隔![]() 个点将下个点染成与原来颜色相反的颜色(称为第
个点将下个点染成与原来颜色相反的颜色(称为第![]() 次染色).
次染色).
(1)对给定正整数![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 次染色后
次染色后![]() 个点均为白色?
个点均为白色?
(2)对给定正整数![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 次染色后
次染色后![]() 个点均为黑色?
个点均为黑色?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年3月,各行各业开始复工复产,生活逐步恢复常态,某物流公司承担从甲地到乙地的蔬菜运输业务.已知该公司统计了往年同期200天内每天配送的蔬菜量X(40≤X<200,单位:件.注:蔬菜全部用统一规格的包装箱包装),并分组统计得到表格如表:
蔬菜量X | [40,80) | [80,120) | [120,160) | [160,200) |
天数 | 25 | 50 | 100 | 25 |
若将频率视为概率,试解答如下问题:
(1)该物流公司负责人决定随机抽出3天的数据来分析配送的蔬菜量的情况,求这3天配送的蔬菜量中至多有2天小于120件的概率;
(2)该物流公司拟一次性租赁一批货车专门运营从甲地到乙地的蔬菜运输.已知一辆货车每天只能运营一趟,每辆货车每趟最多可装载40件,满载才发车,否则不发车.若发车,则每辆货车每趟可获利2000元;若未发车,则每辆货车每天平均亏损400元.为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁几辆货车?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com