考点:函数恒成立问题
专题:
分析:把已知的函数解析式化简变形,得到f(x)=
x++4.然后对k分类求出函数f(x)的值域,结合对定义域内任意实数x
1,x
2,x
3,
不等式f(x
1)+f(x
2)>f(x
3)恒成立,转化值域间的关系列不等式求解k的取值范围.
解答:
解:f(x)=
=
x++4.
当0<k<1时,函数f(x)在[1,3]上为增函数,函数的值域为
[k2+5,+7],
对定义域内任意实数x
1,x
2,x
3,不等式f(x
1)+f(x
2)>f(x
3)恒成立,
即2(k
2+5)≥
+7,
∴0<k<1;
当1≤k≤
时,函数f(x)在[1,3]上的值域为
[2k+4,+7],
对定义域内任意实数x
1,x
2,x
3,不等式f(x
1)+f(x
2)>f(x
3)恒成立,
即4k+8≥
+7,
∴1≤k≤
;
当
≤k≤3时,函数f(x)在[1,3]上的值域为[2k+4,k
2+5],
对定义域内任意实数x
1,x
2,x
3,不等式f(x
1)+f(x
2)>f(x
3)恒成立,
即4k+8≥k
2+5,
∴
≤k≤3;
当k>3时,函数f(x)在[1,3]上为减函数,函数的值域为
[+7,k2+5]对定义域内任意实数x
1,x
2,x
3,不等式f(x
1)+f(x
2)>f(x
3)恒成立,
即
2×(+7)≥k2+5,
∴3
<k≤3.
综上,正数k的范围是:(0,
3].
故答案为:(0,
3].
点评:本题考查了函数恒成立问题,考查了数学转化思想方法,体现了分类讨论的数学思想方法,解答此题的关键在于明确对定义域内任意实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立的意义,是中高档题.



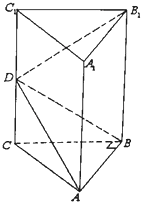 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点