
【题目】已知定点![]() ,动点
,动点![]() 与
与![]() 、
、![]() 两点连线的斜率之积为
两点连线的斜率之积为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知点![]() 是轨迹
是轨迹![]() 上的动点,点
上的动点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() (其中
(其中![]() 为坐标原点),求
为坐标原点),求![]() 面积的最小值.
面积的最小值.
科目:高中数学 来源: 题型:
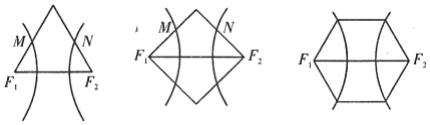
【题目】下列三图中的多边形均为正多边形,![]() ,
,![]() 是所在边的中点,双曲线均以图中的
是所在边的中点,双曲线均以图中的![]() ,
,![]() 为焦点,设图示①②③中的双曲线的离心率分别为
为焦点,设图示①②③中的双曲线的离心率分别为![]() ,
,![]() ,
,![]() 、则
、则![]() ,
,![]() ,
,![]() 的大小关系为( )
的大小关系为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .关于函数
.关于函数![]() 的零点,有下列三个命题:
的零点,有下列三个命题:
①当![]() 时,存在实数m,使函数
时,存在实数m,使函数![]() 恰有5个不同的零点;
恰有5个不同的零点;
②若![]() ,函数
,函数![]() 的零点不超过4个,则
的零点不超过4个,则![]() ;
;
③对![]() ,
,![]() ,函数
,函数![]() 恰有4个不同的零点,且这4个零点可以组成等差数列.
恰有4个不同的零点,且这4个零点可以组成等差数列.
其中,正确命题的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,依此类推,若该数列前
,依此类推,若该数列前![]() 项和
项和![]() 满足:①
满足:①![]() ②
②![]() 是2的整数次幂,则满足条件的最小的
是2的整数次幂,则满足条件的最小的![]() 为
为
A. 21B. 91C. 95D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知平行于
中,已知平行于![]() 轴的动直线
轴的动直线![]() 交抛物线
交抛物线![]() :
: ![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的焦点.圆心不在
的焦点.圆心不在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() ,
, ![]() ,
, ![]() 轴都相切,设
轴都相切,设![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,过
,过![]() 且垂直于
且垂直于![]() 的直线为
的直线为![]() ,直线
,直线![]() ,
, ![]() 分别与
分别与![]() 轴相交于点
轴相交于点![]() ,
, ![]() .当线段
.当线段![]() 的长度最小时,求
的长度最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,定义![]() 为两点
为两点![]() ,
,![]() 之间的“折线距离”.则下列命题中:
之间的“折线距离”.则下列命题中:
①若![]() 点在线段
点在线段![]() 上,则有
上,则有![]()
②若点![]() ,
,![]() ,
,![]() 是三角形的三个顶点,则有
是三角形的三个顶点,则有![]() .
.
③到![]() 两点的“折线距离”相等的点的轨迹是直线
两点的“折线距离”相等的点的轨迹是直线![]() .
.
④若![]() 为坐标原点,
为坐标原点,![]() 在直线
在直线![]() 上,则
上,则![]() 的最小值为
的最小值为![]() .
.
真命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电子阅读的普及,传统纸质媒体遭受到了强烈的冲击.某杂志社近9年来的纸质广告收入如下表所示:

根据这9年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.243;
作线性相关性检验,求得样本相关系数的绝对值为0.243;
根据后5年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.984.
作线性相关性检验,求得样本相关系数的绝对值为0.984.
(1)如果要用线性回归方程预测该杂志社2019年的纸质广告收入,现在有两个方案,
方案一:选取这9年数据进行预测,方案二:选取后5年数据进行预测.
从实际生活背景以及线性相关性检验的角度分析,你觉得哪个方案更合适?
附:相关性检验的临界值表:
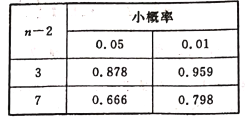
(2)某购物网站同时销售某本畅销书籍的纸质版本和电子书,据统计,在该网站购买该书籍的大量读者中,只购买电子书的读者比例为![]() ,纸质版本和电子书同时购买的读者比例为
,纸质版本和电子书同时购买的读者比例为![]() ,现用此统计结果作为概率,若从上述读者中随机调查了3位,求购买电子书人数多于只购买纸质版本人数的概率.
,现用此统计结果作为概率,若从上述读者中随机调查了3位,求购买电子书人数多于只购买纸质版本人数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com