
【题目】已知曲线C在直角坐标系xOy下的参数方程为 ![]() (θ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(θ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程; (Ⅱ)直线l的极坐标方程是ρcos(θ﹣ ![]() )=3
)=3 ![]() ,射线OT:θ=
,射线OT:θ= ![]() (ρ>0)与曲线C交于A点,与直线l交于B,求线段AB的长.
(ρ>0)与曲线C交于A点,与直线l交于B,求线段AB的长.
【答案】
(1)解:(1)曲线C的参数方程为 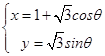 (θ为参数),
(θ为参数),
消去参数化为:(x﹣1)2+y2=3,展开为:x2+y2﹣2x﹣2=0,
化为极坐标方程:ρ2﹣2ρcosθ﹣2=0.
(II)联立 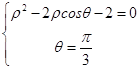 ,化为:ρ2﹣ρ﹣2=0,ρ>0,解得ρ=2.
,化为:ρ2﹣ρ﹣2=0,ρ>0,解得ρ=2.
射线OT:θ= ![]() (ρ>0)与曲线C交于A点
(ρ>0)与曲线C交于A点 ![]() .
.
联立 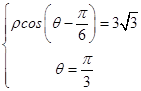 ,
,
解得ρ=6,射线OT:θ= ![]() (ρ>0)与直线l交于B
(ρ>0)与直线l交于B ![]() ,
,
∴线段AB的长=6﹣2=4
【解析】(1)曲线C的参数方程为 ![]() (θ为参数),消去参数化为:(x﹣1)2+y2=3,展开利用互化公式即可得出极坐标方程.(II)射线OT:θ=
(θ为参数),消去参数化为:(x﹣1)2+y2=3,展开利用互化公式即可得出极坐标方程.(II)射线OT:θ= ![]() (ρ>0)分别与曲线C,直线l的极坐标方程联立解出交点坐标即可得出.
(ρ>0)分别与曲线C,直线l的极坐标方程联立解出交点坐标即可得出.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.经过点P0(x0 , y0)的直线都可以用方程y-y0=k(x-x0)表示
B.经过定点A(0,b)的直线都可以用方程y=kx+b表示
C.经过任意两个不同点P1(x1 , y1),P2(x2 , y2)的直线都可用方程(x2-x1)(y-y1)=(y2-y1)(x-x1)表示
D.不经过原点的直线都可以用方程 ![]() 表示
表示
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线方程为16x2﹣9y2=144.
(1)求该双曲线的实轴长、虚轴长、离心率;
(2)若抛物线C的顶点是该双曲线的中心,而焦点是其左顶点,求抛物线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点.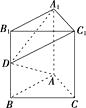
求证:AD⊥平面A1DC1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 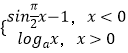 (a>0且a≠1)的图象上关于y轴对称的点至少有3对,则实数a的范围是( )
(a>0且a≠1)的图象上关于y轴对称的点至少有3对,则实数a的范围是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.(0, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com