
【题目】已知函数![]() .
.
(1)讨论函数f(x)的单调性;
(2)若函数g(x)=f(x)﹣lnx有2个不同的极值点x1,x2(x1<x2),求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)求导得到![]() ,讨论
,讨论![]() 四种情况得到单调性.
四种情况得到单调性.
(2)g(x)=alnx![]() x﹣1,
x﹣1,![]() ,得到x1+x2=a,x1x2=a,f(x1)+f(x2)﹣2x1x2=alna+lna﹣2a﹣2,设g(a)=alna+lna﹣2a﹣2,(a>4),根据函数的单调性得到答案.
,得到x1+x2=a,x1x2=a,f(x1)+f(x2)﹣2x1x2=alna+lna﹣2a﹣2,设g(a)=alna+lna﹣2a﹣2,(a>4),根据函数的单调性得到答案.
(1)![]() ,x>0,
,x>0,
(i)若a=1,![]() 0恒成立,故f(x)在(0,+∞)单调递减,
0恒成立,故f(x)在(0,+∞)单调递减,
(ii)当a>1时,x∈(0,1)时,f′(x)<0,函数单调递减,当x∈(1,a),f′(x)>0,函数单调递增,当x∈(a,+∞),f′(x)<0,函数单调递减,
(iii)0<a<1时,x∈(0,a)时,f′(x)<0,函数单调递减,当x∈(a,1),f′(x)>0,函数单调递增,当x∈(1,+∞),f′(x)<0,函数单调递减,
(iv)当a≤0时,x∈(0,1)时,f′(x)>0,函数单调递增,当x∈(1,+∞),f′(x)<0,函数单调递减.
(2)g(x)=f(x)﹣lnx=alnx![]() x﹣1,
x﹣1,![]() ,
,
由题意可得,x2﹣ax+a=0与2个不同的根x1,x2(x1<x2),
则x1+x2=a>0,x1x2=a,△=a2﹣4a>0,所以a>4,
∴f(x1)+f(x2)﹣2x1x2=a(lnx1+lnx2)+a(![]() )+(lnx1+lnx2)﹣(x1+x2)﹣2﹣2x1x2=alna+lna﹣2a﹣2,
)+(lnx1+lnx2)﹣(x1+x2)﹣2﹣2x1x2=alna+lna﹣2a﹣2,
令g(a)=alna+lna﹣2a﹣2,(a>4),
则![]() 2=lna
2=lna![]() 1>0,即g(a)在(4,+∞)上单调递增,
1>0,即g(a)在(4,+∞)上单调递增,
所以g(a)>g(4)=5ln4﹣10=5(ln4﹣2)=5(ln4﹣lne2)=5![]() .得证.
.得证.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
【题目】某市为了调查小区成年居民对环境治理情况的满意度(满分按100计),随机对20名六十岁以上的老人和20名十八岁以上六十岁以下的中青年进行了不记名的问卷调查,得到了如下统计结果:
表1:六十岁以上的老人对环境治理情况的满意度与频数分布表
满意度 |
|
|
|
|
|
人数 | 1 | 5 | 6 | 5 | 3 |
表2:十八岁以上六十岁以下的中青年人对环境治理情况的满意度与频数分布表
满意度 |
|
|
|
|
|
人数 | 2 | 4 | 8 | 4 | 2 |
表3:
满意度小于80 | 满意度不小于80 | 合计 | |
六十岁以上老人人数 | |||
十八岁以上六十岁以下的中青年人人数 | |||
合计 |
(1)若该小区共有中青年人500人,试估计其中满意度不少于80的人数;
(2)完成表3的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“小区成年居民对环境治理情况的满意度与年龄有关”?
的把握认为“小区成年居民对环境治理情况的满意度与年龄有关”?
(3)从表3的六十岁以上的老人“满意度小于80”和“满意度不小于80”的人数中用分层抽样的方法抽取一个容量为5的样本,再从中任取3人,求至少有两人满意小于80的概率.
附: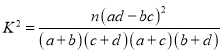 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (其中
(其中![]() ,m,n为常数)
,m,n为常数)
(1)当![]() 时,对
时,对![]() 有
有![]() 恒成立,求实数n的取值范围;
恒成立,求实数n的取值范围;
(2)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,函数
,函数![]() 的零点为
的零点为![]() ,求所有满足
,求所有满足![]() 的整数k的和.
的整数k的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“斗拱”是中国古代建筑中特有的构件,从最初的承重作用,到明清时期集承重与装饰作用于一体.在立柱顶、额枋和檐檩间或构架间,从枋上加的一层层探出成弓形的承重结构叫拱拱与拱之间垫的方形木块叫斗.如图所示,是“散斗”(又名“三才升”)的三视图(三视图中的单位:分米),现计划用一块长方体的海南黄花梨木料加工成该散斗,则长方体木料的最小体积为( )立方分米.
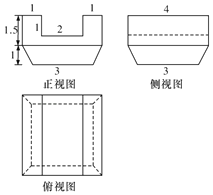
A.40B.![]() C.30D.
C.30D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|,a∈R.
(1)当f(2)+f(﹣2)>4时,求a的取值范围;
(2)若a>0,x,y∈(﹣∞,a],不等式f(x)≤|y+3|+|y﹣a|恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 (t为参数,a∈R).在以坐标原点为极点,x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为
(t为参数,a∈R).在以坐标原点为极点,x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)若点A(0,4)在直线l上,求直线l的极坐标方程;
(2)已知a>0,若点P在直线l上,点Q在曲线C上,若|PQ|最小值![]() 为,求a的值.
为,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在创建“全国文明卫生城”过程中,运城市“创城办”为了调查市民对创城工作的了解情况,进行了一次创城知识问卷调查(一位市民只能参加一次),通过随机抽样,得到参加问卷调查的![]() 人的得分统计结果如表所示:.
人的得分统计结果如表所示:.
组别 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)由频数分布表可以大致认为,此次问卷调查的得分![]() 似为这
似为这![]() 人得分的平均值(同一组中的数据用该组区间的中点值作代表),利用该正态分布,求
人得分的平均值(同一组中的数据用该组区间的中点值作代表),利用该正态分布,求![]() ;
;
(2)在(1)的条件下,“创城办”为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() 的可以获赠
的可以获赠![]() 次随机话费,得分低于
次随机话费,得分低于![]() 的可以获赠
的可以获赠![]() 次随机话费;
次随机话费;
②每次获赠的随机话费和对应的概率为:
赠送话费的金额(单位:元) |
|
|
概率 |
|
|
现有市民甲参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:参考数据与公式:![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的中心为坐标原点
的中心为坐标原点![]() 焦点在
焦点在![]() 轴上,右顶点
轴上,右顶点![]() 到右焦点的距离与它到右准线的距离之比为
到右焦点的距离与它到右准线的距离之比为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两点,设
轴对称的任意两点,设![]() ,连接
,连接![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .求证:直线
.求证:直线![]() 过定点
过定点![]() 并求出点
并求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,E为线段
,E为线段![]() 的中点.
的中点.
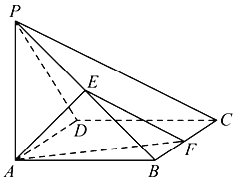
(1)证明:点F在线段![]() 上移动时,
上移动时,![]() 为直角三角形;
为直角三角形;
(2)若F为线段![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com