
����Ŀ��ij����һ��ֱ�������εؿ飬�ּƻ����������һ����κ�����������������ͼ�����������������ֳ���ʩ�Ľ��裬������BCD����������ֲ���ֹ��ͻ��ܣ�������CAE����������ֲ���ֹ��ͻ��ܣ���֪OA=4ǧ�ף�OB=3ǧ�ף���AOB=90�㣬���ֻ���ÿƽ��ǧ�����1��Ԫ�����ֻ���ÿƽ��ǧ�����4��Ԫ����OE=xǧ�ף��Խ�����ֲ���ܵ������Ϊy����λ����Ԫ������x�ĺ�����ϵʽ����xΪ��ֵʱ����ֲ���ܵ��������С�����������ۣ� 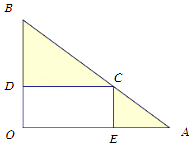
���𰸡��⣺�����⣬CD=OE=x���ɡ�BCD�ס�BAO֪BD= ![]() x������S��BCD=
x������S��BCD= ![]() x2 ��
x2 ��
ͬ����S��CAE= ![]() ��x��4��2
��x��4��2
���ԣ�y= ![]() [x2+��x��4��2��4]=
[x2+��x��4��2��4]= ![]() ��5x2��32x+64��������0��x��4��
��5x2��32x+64��������0��x��4��
y= ![]() [5��x��
[5��x�� ![]() ��2+
��2+ ![]() ]
]
��Ϊ0����4����14��
����x= ![]() ʱ��y����СֵΪ4.8��Ԫ��
ʱ��y����СֵΪ4.8��Ԫ��
��xΪ ![]() ʱ����ֲ���ܵ��������С���������СֵΪ4.8��Ԫ
ʱ����ֲ���ܵ��������С���������СֵΪ4.8��Ԫ
�����������������BCD��������CAE�����������ɵú�������ʽ�������䷽�����ɵú�������ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Բ
��������Բ![]() �ϵĵ�
�ϵĵ�![]() �ġ�����㡱Ϊ
�ġ�����㡱Ϊ![]() .
.
��1������Բ![]() �ϵĵ�
�ϵĵ�![]() �ġ�����㡱
�ġ�����㡱![]() �Ĺ켣���̣�
�Ĺ켣���̣�
��2�������Բ![]() �ϵĵ�
�ϵĵ�![]() �ġ�����㡱Ϊ
�ġ�����㡱Ϊ![]() ��������Բ
��������Բ![]() �ϵ������
�ϵ������![]() �����ġ�����㡱
�����ġ�����㡱![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ��
�� ![]() ʱ��ֱ��
ʱ��ֱ��![]() ����Բ
����Բ![]() ��
��![]() ��
�� ![]() ���㣬����
���㣬����![]() ��
�� ![]() �ġ�����㡱�ֱ���
�ġ�����㡱�ֱ���![]() ��
�� ![]() ������
������![]() Ϊֱ����Բ��������ԭ��
Ϊֱ����Բ��������ԭ��![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ��
�� ![]() ���
���![]() ��
�� ![]() ����
����![]() ��
�� ![]() �ֱ�Ϊ���ҽ������Բ
�ֱ�Ϊ���ҽ������Բ![]() ��
�� ![]() ������Բ�Ľ��㡣
������Բ�Ľ��㡣
��������Բ![]() �ķ��̣�
�ķ��̣�
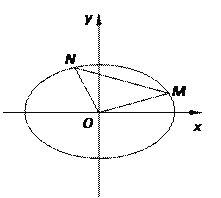
����![]() ��
��![]() ����Բ
����Բ![]() �ϵ����㣬��ֱ��
�ϵ����㣬��ֱ��![]() ��
��![]() ��б��֮��Ϊ
��б��֮��Ϊ![]() ������
������![]() ������Ƿ�Ϊ��ֵ�����ǣ���������ֵ�������ǣ���˵�����ɡ�
������Ƿ�Ϊ��ֵ�����ǣ���������ֵ�������ǣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={x|��1��x��10}������B={x|2x��6��0}��
��R��A��B����
��֪C={x|a��x��a+1}����CA����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�ü��������������ȡ��30��ͬѧ������ÿ��ƽ�������Ķ�ʱ�䣨��λ��Сʱ�����е��飬��Ҷͼ��ͼ��
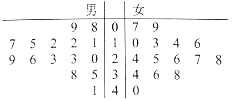
�����¾������Ķ�ʱ�䲻����30Сʱ��ѧ����Ϊ�������ԡ�.
��1����Ƶ����Ϊ���ʣ����Ƹ�У900��ѧ���С������ԡ��ж����ˣ�
��2�����ѳ�ȡ��7���������ԡ��������ȡ�С�Ů�������ԡ���1�ˣ��μӶ����������.
��i�����ж����ֲ�ͬ�ij�ȡ������
��ii�����ȡ���С�Ů��λ�������ԡ��¾�����ʱ��������2Сʱ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
�ڼ�����ϵ�У��� ![]() �ļ�������
�ļ�������![]() ������
������ ![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .�Լ���Ϊ����ԭ�㣬����Ϊ
.�Լ���Ϊ����ԭ�㣬����Ϊ ![]() ��������Ὠ��ƽ��ֱ������ϵ��б��Ϊ
��������Ὠ��ƽ��ֱ������ϵ��б��Ϊ ![]() ��ֱ��
��ֱ�� ![]() ������
������![]() .
.
��1��д��ֱ�� ![]() �IJ������̺�����
�IJ������̺����� ![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2����ֱ�� ![]() ������
������![]() �ཻ������
�ཻ������![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ݺ���f��x��=����2m2+m+2��xm+1Ϊż������
��1����f��x���Ľ���ʽ��
��2��������y=f��x����2��a��1��x+1�����䣨2��3����Ϊ������������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��
����![]() ʱ����֤������
ʱ����֤������![]() ������ֱ��������
������ֱ��������![]() ���У�
����
����![]() ʱ��
ʱ�� ![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ������
������ ![]() ������f��x��=
������f��x��= ![]() ��
��
��1������f��x���ĵ����������䣻
��2��������y=f��x����ͼ�������е�����ƽ���ƶ� ![]() ����λ���ȣ��ú���y=g��x����ͼ������y=g��x��������[0����]�ϵ�ֵ��
����λ���ȣ��ú���y=g��x����ͼ������y=g��x��������[0����]�ϵ�ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com