Question

正方体的八个顶点中有4个顶点恰好是正四面体的顶点，则正方体的边长与正四面体的边长之比是    ．

Answer 1

【答案】分析：由正方体的八个顶点中有4个顶点恰好是正四面体的顶点，知该正四面体恰好以正方体的面对角线为棱，由此能求出正方体的边长与正四面体的边长之比．
解答：解：∵正方体的八个顶点中有4个顶点恰好是正四面体的顶点，
∴该正四面体恰好以正方体的面对角线为棱，
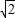
设正方体的棱长为a，则正四面体的棱长为a，
∴正方体的边长与正四面体的边长之比是1：．
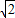
故答案为：1：．
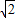
点评：本题考查正方体的边长与正四面体的边长之比的求法，解题时要认真审题，注意熟练掌握正方体的结构特征．