
分析 (1)利用二次函数的零点,代入方程,化简求解即可.
(2)求出函数f(x)的最小值,即可求解k的范围.
(3)问题转化为r=1+2•($\frac{1}{{2}^{x}}$)2-3•$\frac{1}{{2}^{x}}$在x∈[-1,1]上有解,通过换元得到r=2t2-3t+1在t∈[$\frac{1}{2}$,2]上有解,求出k的范围即可.
解答 解:(1)函数f(x)=x2-3mx+n(m>0)的两个零点分别为1和2.
可得:1-3m+n=0,4-6m+n=0,解得m=1,n=2,
(2)由(1)可得f(x)=x2-3x+2,
不等式f(x)-k>0在x∈[0,5]恒成立,
可得不等式f(x)>k在x∈[0,5]恒成立,
f(x)=x2-3x+2在x∈[0,5]上的最小值为:f($\frac{3}{2}$)=-$\frac{1}{4}$,
可得k<-$\frac{1}{4}$.
(3)$g(x)=\frac{f(x)}{x}$=x+$\frac{2}{x}$-3,函数F(x)=g(2x)-r•2x在x∈[-1,1]上有零点,
即g(2x)-r•2x=0在x∈[-1,1]上有解,
即r=1+2•($\frac{1}{{2}^{x}}$)2-3•$\frac{1}{{2}^{x}}$在x∈[-1,1]上有解,
令t=$\frac{1}{{2}^{x}}$,则r=2t2-3t+1,
∵x∈[-1,1],∴t∈[$\frac{1}{2}$,2],
即r=2t2-3t+1在t∈[$\frac{1}{2}$,2]上有解,
r=2k2-2t+1=2(t-$\frac{3}{4}$)2-$\frac{1}{8}$,($\frac{1}{2}$≤t≤2),
∴-$\frac{1}{8}$≤r≤3,
∴r的范围是[-$\frac{1}{8}$,3].
点评 本题考查了二次函数的性质,考查函数的单调性、最值问题,考查换元思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
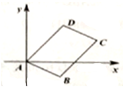 如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限.
如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$-\frac{1}{3}$) | B. | (-$\frac{1}{3}$,$\frac{1}{3}$) | C. | ($-\frac{1}{3}$,1] | D. | ($-\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 130万元 | B. | 130.25万元 | C. | 120万元 | D. | 100万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3{y}^{2}}{4}$-$\frac{{x}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{2}$-$\frac{3{y}^{2}}{2}$=1 | C. | $\frac{5{y}^{2}}{3}$-x2=1 | D. | $\frac{3{y}^{2}}{2}$-$\frac{{x}^{2}}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<p<q<n | B. | p<m<q<n | C. | m<p<n<q | D. | p<m<n<q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com