
【题目】已知数列{an}的前n项和为Sn , 且n+1=1+Sn对一切正整数n恒成立.
(1)试求当a1为何值时,数列{an}是等比数列,并求出它的通项公式;
(2)在(1)的条件下,当n为何值时,数列 ![]() 的前n项和Tn取得最大值.
的前n项和Tn取得最大值.
【答案】
(1)解:由an+1=1+Sn得:当n≥2时,an=1+Sn﹣1,
两式相减得:an+1=2an,
∵数列{an}是等比数列,∴a2=2a1,
又∵a2=1+S1=1+a1,解得:a1=1.
得: ![]()
(2)解: ![]() ,可知数列
,可知数列 ![]() 是一个递减数列,
是一个递减数列,
∴ ![]() ,
,
由此可知当n=9时,数列 ![]() 的前项和Tn取最大值
的前项和Tn取最大值
【解析】1、根据题意由an+1=1+Sn,推导出等比数列{an}的公比q=2,再根据等比数列的通项公式求得。
2、由题意可得数列 { l g ![]() } 是一个递减数列,根据题意可得前8项为正,故当n=9时数列的前项和Tn取最大值。
} 是一个递减数列,根据题意可得前8项为正,故当n=9时数列的前项和Tn取最大值。
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系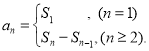 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为迎接今年6月6日的“全国爱眼日”,某高中学校学生会随机抽取16名学生,经校 医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如右图,若视力测试结果不低于5.0,则称为“好视力”, 
(1)写出这组数据的众数和中位数;
(2)求从这16人中随机选取3人,至少有2人是“好视力”的概率;
(3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记X表示抽到“好视力”学生的人数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() ,其离心率
,其离心率 ![]() ,点
,点 ![]() 为椭圆上的一个动点,△
为椭圆上的一个动点,△ ![]() 面积的最大值为
面积的最大值为 ![]() .
.
(1)求椭圆的标准方程;
(2)若 ![]() 是椭圆上不重合的四个点,
是椭圆上不重合的四个点, ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,
, ![]() 求
求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1 , a14=b4 .
(1)求{an}的通项公式;
(2)设cn=an+bn , 求数列{cn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组有9名学生.若从9名学生中选取3人,则选取的3人中恰好有一个女生的概率是 ![]() .
.
(1)该小组中男女学生各多少人?
(2)9个学生站成一列队,现要求女生保持相对顺序不变(即女生 前后顺序保持不变)重新站队,问有多少种重新站队的方法?(要求用数字作答)
(3)9名学生站成一列,要求男生必须两两站在一起,有多少种站队的方法?(要求用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】底面为正方形的四棱锥S﹣ABCD,且SD⊥平面ABCD,SD= ![]() ,AB=1,线段SB上一M点满足
,AB=1,线段SB上一M点满足 ![]() =
= ![]() ,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成的.已知半球的直径是6 cm,圆柱筒高为2 cm.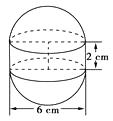
(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?
(2)要在2 500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com