
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() ,
,![]() .
.
(1)若![]() 为等边三角形,求椭圆
为等边三角形,求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的短轴长为2,过点
的短轴长为2,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
试题分析:(1)由![]() 为等边三角形可得a=2b,又c=1,集合
为等边三角形可得a=2b,又c=1,集合![]() 可求
可求![]() ,则椭圆C的方程可求;(2)由给出的椭圆C的短轴长为2,结合c=1求出椭圆方程,分过点F2的直线l的斜率存在和不存在讨论,当斜率存在时,把直线方程和椭圆方程联立,由根与系数关系写出两个交点的横坐标的和,把
,则椭圆C的方程可求;(2)由给出的椭圆C的短轴长为2,结合c=1求出椭圆方程,分过点F2的直线l的斜率存在和不存在讨论,当斜率存在时,把直线方程和椭圆方程联立,由根与系数关系写出两个交点的横坐标的和,把
![]() 转化为数量积等于0,代入坐标后可求直线的斜率,则直线l的方程可求
转化为数量积等于0,代入坐标后可求直线的斜率,则直线l的方程可求
试题解析:(1)![]() 为等边三角形,则
为等边三角形,则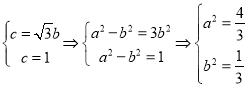 ……2
……2
椭圆![]() 的方程为:
的方程为:![]() ; ……3
; ……3
(2)容易求得椭圆![]() 的方程为
的方程为![]() , ……5
, ……5
当直线![]() 的斜率不存在时,其方程为
的斜率不存在时,其方程为![]() ,不符合题意; ……6
,不符合题意; ……6
当直线的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由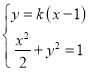 得
得![]() ,设
,设![]() ,
,
则![]() , ……8
, ……8
![]() ∵
∵![]() ,
,
∴![]() ,
,
即![]()
![]() ……10
……10
解得![]() ,即
,即![]() ,
,
故直线![]() 的方程为
的方程为![]() 或
或![]() . ……12
. ……12


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,
,![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,
,![]() ,切点分别为
,切点分别为![]() ,
,![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋中装有4个形状大小完全相同的小球,小球的编号分别为1,2,3,4,甲、乙依次有放回地随机抽取1个小球,取到小球的编号分别为![]() .在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,则甲、乙两人成为“好朋友”的概率为__________.
.在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,则甲、乙两人成为“好朋友”的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以椭圆![]() 的四个顶点为顶点的四边形的四条边与
的四个顶点为顶点的四边形的四条边与![]() 共有
共有![]() 个交点,且这
个交点,且这![]() 个交点恰好把圆周六等分.
个交点恰好把圆周六等分.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 相切,且椭圆
相切,且椭圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com