
【题目】已知函数f(x)=lnx﹣ ![]() a(x﹣1)(a∈R).
a(x﹣1)(a∈R).
(1)若a=﹣2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若不等式f(x)<0对任意x∈(1,+∞)恒成立. (ⅰ)求实数a的取值范围;
(ⅱ)试比较ea﹣2与ae﹣2的大小,并给出证明(e为自然对数的底数,e=2.71828).
【答案】
(1)解:因为a=﹣2时,f(x)=inx+x﹣1, ![]() .
.
所以切点为(1,0),k=f′(1)=2.
所以a=﹣2时,曲线y=f(x)在点(1,f(1))处的切线方程为y=2x﹣2.
(2)解:( i)由f(x)=lnx﹣ ![]() a(x﹣1),
a(x﹣1),
所以 ![]() ,
,
①当a≤0时,x∈(1,+∞),f′(x)>0,
∴f(x)在(1,+∞)上单调递增,f(x)>f(1)=0,
∴a≤0不合题意.
②当a≥2即 ![]() 时,
时, ![]() 在(1,+∞)上恒成立,
在(1,+∞)上恒成立,
∴f(x)在(1,+∞)上单调递减,有f(x)<f(1)=0,
∴a≥2满足题意.
③若0<a<2即 ![]() 时,由f′(x)>0,可得
时,由f′(x)>0,可得 ![]() ,由f′(x)<0,可得x
,由f′(x)<0,可得x ![]() ,
,
∴f(x)在 ![]() 上单调递增,在
上单调递增,在 ![]() 上单调递减,
上单调递减,
∴ ![]() ,
,
∴0<a<2不合题意.
综上所述,实数a的取值范围是[2,+∞).
( ii)a≥2时,“比较ea﹣2与ae﹣2的大小”等价于“比较a﹣2与(e﹣2lna)的大小”
设g(x)=x﹣2﹣(e﹣2)lnx,(x≥2).
则 ![]() .
.
∴g(x)在[2,+∞)上单调递增,因为g(e)=0.
当x∈[2,e)时,g(x)<0,即x﹣2<(e﹣2)lnx,所以ex﹣2<xe﹣2.
当x∈(e,+∞)时g(x)>0,即x﹣2>(e﹣2)lnx,∴ex﹣2>xe﹣2.
综上所述,当a∈[2,e)时,ea﹣2<ae﹣2;
当a=e时,ea﹣2=ae﹣2;
当a∈(e,+∞)时,ea﹣2>ae﹣2
【解析】(1)一求切点,二求切点处的导数,即切线的斜率;(2)只需求出函数f(x)在区间[1,+∞)上的最大值即可,利用导数研究单调性,进一步求其最值构造不等式求解;比较大小可将两个值看成函数值,然后利用函数的性质求解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在中学生综合素质评价某个维度的测评中,分优秀、合格、尚待改进三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表一:男生

表二:女生

(1)从表二的非优秀学生中随机抽取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下面的![]() 列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.

参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ),焦点
),焦点![]() 到准线的距离为
到准线的距离为![]() ,过点
,过点![]()
![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于点
于点![]() (点
(点![]() 在第一象限).
在第一象限).
(Ⅰ)若点![]() 焦点
焦点![]() 重合,且弦长
重合,且弦长![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)若点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 交x轴于点
交x轴于点![]() ,且
,且![]() ,求证:点B的坐标是
,求证:点B的坐标是![]() ,并求点
,并求点![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学刚搬迁到新校区,学校考虑,若非住校生上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课.为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如下频率分布直方图,其中时间分组为[0,10),[10,20),[20,30),[30,40),[40,50]. 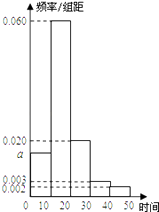
(1)求频率分布直方图中a的值;
(2)从统计学的角度说明学校是否需要推迟5分钟上课;
(3)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求恰有一个学生的单程时间落在[40,50]上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个袋子,其中甲袋中装有编号分别为1、2、3、4的4个完全相同的球,乙袋中装有编号分别为2、4、6的3个完全相同的球.
(Ⅰ)从甲、乙袋子中各取一个球,求两球编号之和小于8的概率;
(Ⅱ)从甲袋中取2个球,从乙袋中取一个球,求所取出的3个球中含有编号为2的球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 7 | 8 | 9 | 10 | 11 | 12 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据7至11月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,参考数据:
,参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若钝角三角形的三边长和面积都是整数,则称这样的三角形为“钝角整数三角形”,下列选项中能构成一个“钝角整数三角形”三边长的是( )
A.2,3,4
B.2,4,5
C.5,5,6
D.4,13,15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( ) 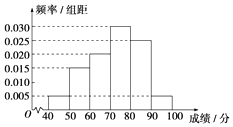
A.73.3,75,72
B.72,75,73.3
C.75,72,73.3
D.75,73.3,72
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com