
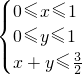 下,函数
下,函数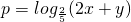 的最小值为________.
的最小值为________.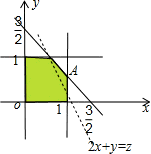 解:(文) 不等式表示的可行域如图设2x+y=z.变形为y=-2x+z,
解:(文) 不等式表示的可行域如图设2x+y=z.变形为y=-2x+z,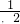 )时,l在y轴上截距z最大,从而2x+y 最大,
)时,l在y轴上截距z最大,从而2x+y 最大, =
= ,∴函数
,∴函数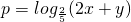 的最小值为 lo
的最小值为 lo
 =-1.
=-1. :
: =3:1.
=3:1.

科目:高中数学 来源: 题型:
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| mx |
| m+1-x |
| 1 |
| 2 |
| 1 |
| xn |
| 1 |
| 2 |
| 1 |
| xn |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年湖北黄冈联考文)(12分)
已知二次函数![]() 满足条件:①
满足条件:①![]() ; ②
; ②![]() 的最小值为
的最小值为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设数列![]() 的前
的前![]() 项积为
项积为![]() , 且
, 且![]() , 求数列
, 求数列![]() 的通项公式;
的通项公式;
(Ⅲ) 在(Ⅱ)的条件下, 若![]() 是
是![]() 与
与![]() 的等差中项, 试问数列
的等差中项, 试问数列![]() 中第几项的
中第几项的
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com