
【题目】已知函数![]() .
.
(1)若函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的最小值;
的最小值;
(2)若函数![]() 在区间
在区间![]() 上无零点,求实数
上无零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1) 求出![]() ,分两种情况讨论
,分两种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,令
增区间,令![]() 是所求区间的子集即可得结果;(2)“函数
是所求区间的子集即可得结果;(2)“函数![]() 在区间
在区间![]() 上无零点”等价于“函数
上无零点”等价于“函数![]() 与
与![]() 的图象在
的图象在![]() 上没有公共点”,讨论三种情况,分别画出函数的图象,结合直线过定点,即可求得实数
上没有公共点”,讨论三种情况,分别画出函数的图象,结合直线过定点,即可求得实数![]() 的取值范围.
的取值范围.
详解:(1) 函数![]() 的定义域为
的定义域为![]() ,
,![]()
讨论:
当![]() 时,
时,![]() ,
,
此时函数![]() 在
在![]() 上单调递增,满足题设;
上单调递增,满足题设;
当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
所以此时函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
又函数![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() ,解得
,解得![]() ,
,
综上,实数![]() 的最小值是
的最小值是![]() .
.
(2)由![]() ,得
,得![]()
设![]() ,则“函数
,则“函数![]() 在区间
在区间![]() 上无零点”等价于“函数
上无零点”等价于“函数![]() 与
与![]() 的图象在
的图象在![]() 上没有公共点”
上没有公共点”
讨论:
当![]() 时,
时,![]() 在
在![]() 上是单调递增函数,函数
上是单调递增函数,函数![]() 在
在![]() 上也是单调递增函数,
上也是单调递增函数,
作出函数![]() 与函数
与函数![]() 满足题意的草图(草图可能有两种情况)如下:
满足题意的草图(草图可能有两种情况)如下:
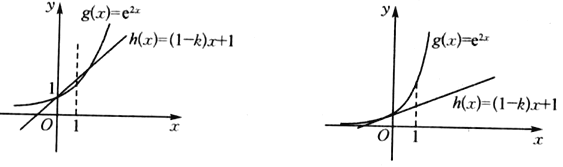
图1 图2
(i)如图1,![]() ,即
,即![]() ,解得
,解得![]() ;
;
(ii)如图2,![]() 对任意
对任意![]() 恒成立
恒成立
又当![]() 时,
时,![]() ,所以
,所以![]() ,解得
,解得![]()
又![]() ,得
,得![]()
综上,![]() 或
或![]() ;
;
当![]() 时,符合题意;
时,符合题意;
当![]() 时,
时,![]() 在
在![]() 上是单调递减函数,
上是单调递减函数,![]() 在
在![]() 上是单调递增函数,
上是单调递增函数,
作出函数![]() 与函数
与函数![]() 满足题意的草图如下:
满足题意的草图如下:
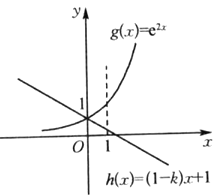
观察图象可知![]() 符合题意.
符合题意.
综上,所求实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】新生婴儿性别比是每100名女婴对应的男婴数.通过抽样调查得知,我国2014年、2015年出生的婴儿性别比分别为115.88和113.51.
(1)分别估计我国2014年和2015年男婴的出生率(新生儿中男婴的比率,精确到0.001);
(2)根据估计结果,你认为“生男孩和生女孩是等可能的”这个判断可靠吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面ABCD为直角梯形,
中,底面ABCD为直角梯形,![]() ,
,![]() ,
,![]() ,点E为AD的中点,
,点E为AD的中点,![]() ,
,![]() 平面ABCD,且
平面ABCD,且![]()

![]() 求证:
求证:![]() ;
;
![]() 线段PC上是否存在一点F,使二面角
线段PC上是否存在一点F,使二面角![]() 的余弦值是
的余弦值是![]() ?若存在,请找出点F的位置;若不存在,请说明理由.
?若存在,请找出点F的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个试验中,把一种血清注射到500只豚鼠体内,被注射前,这些豚鼠中150只有圆形细胞,250只有椭圆形细胞,100只有不规则形状细胞;被注射后,没有一个具有圆形细胞的豚鼠被感染,50个具有椭圆形细胞的豚鼠被感染,具有不规则形状细胞的豚鼠全部被感染,根据试验结果,估计具有下列类型的细胞的豚鼠被这种血清感染的概率;
(1)圆形细胞;
(2)椭圆形细胞;
(3)不规则形状细胞.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水域受到污染,水务部门决定往水中投放一种药剂来净化水质,已知每次投放质量为![]() 的药剂后,经过
的药剂后,经过![]() (
(![]() )天,该药剂在水中释放的浓度
)天,该药剂在水中释放的浓度![]() (毫克
(毫克![]() 升)为
升)为![]() ,其中
,其中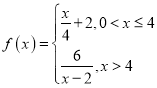 ,当药剂在水中释放浓度不低于
,当药剂在水中释放浓度不低于![]() (毫克
(毫克![]() 升)时称为有效净化,当药剂在水中释放的浓度不低于
升)时称为有效净化,当药剂在水中释放的浓度不低于![]() (毫克
(毫克![]() 升)且不高于
升)且不高于![]() (毫克
(毫克![]() 升)时称为最佳净化.
升)时称为最佳净化.
(1)如果投放的药剂质量为![]() ,那么该水域达到有效净化一共可持续几天?
,那么该水域达到有效净化一共可持续几天?
(2)如果投放的药剂质量为![]() ,为了使该水域
,为了使该水域![]() 天(从投放药剂算起,包括第
天(从投放药剂算起,包括第![]() 天)之内都达到最佳净化,确定应该投放的药剂质量
天)之内都达到最佳净化,确定应该投放的药剂质量![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com