
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| PF1 |
| PF2 |
| 11 |
| 4 |
| 3 |
| 2 |
| AE |
| BE |
| 2 |
| 2 |
| PF1 |
| PF2 |
| 2 |
| 2 |
| x2 |
| 2 |
| 2 |
| PF1 |
| PF2 |
| x2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| PF1 |
| PF2 |
| 3 |
| 2 |
| -8k |
| 1+2k2 |
| 6 |
| 1+2k2 |
| 2k2-4 |
| 2k2+1 |
| 4 |
| 2k2+1 |
| 11 |
| 4 |
| AE |
| 11 |
| 4 |
| BE |
| 11 |
| 4 |
| AE |
| BE |
| 121 |
| 16 |
| 11 |
| 4 |
| 6 |
| 1+2k2 |
| 121 |
| 16 |
| 11 |
| 4 |
| 4 |
| 2k2+1 |
| 2k2-4 |
| 2k2+1 |
| 105 |
| 16 |
| 3 |
| 2 |
| AE |
| BE |


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
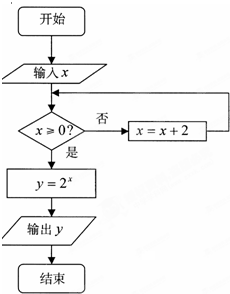 如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )
如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )A、
| ||
B、
| ||
| C、2 | ||
| D、8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| y |
| x+2 |
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com