
【题目】潍坊文化艺术中心的观光塔是潍坊市的标志性建筑,某班同学准备测量观光塔![]() 的高度
的高度![]() (单位:米),如图所示,垂直放置的标杆
(单位:米),如图所示,垂直放置的标杆![]() 的高度
的高度![]() 米,已知
米,已知![]() ,
, ![]() .
.
(1)该班同学测得![]() 一组数据:
一组数据: ![]() ,请据此算出
,请据此算出![]() 的值;
的值;
(2)该班同学分析若干测得的数据后,发现适当调整标杆到观光塔的距离![]() (单位:米),使
(单位:米),使![]() 与
与![]() 的差较大,可以提高测量精确度,若观光塔高度为136米,问
的差较大,可以提高测量精确度,若观光塔高度为136米,问![]() 为多大时,
为多大时, ![]() 的值最大?
的值最大?

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】一批材料可以建成100m长的围墙,现用这些材料在一边靠墙的地方围成一块封闭的矩形场地,中间隔成3个面积相等的小矩形(如图),则围成的矩形场地的最大总面积为(围墙厚度忽略不计)m2 . 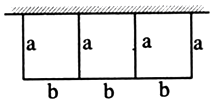
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() ,函数
,函数![]() ,
, ![]() .
.
(Ⅰ)若![]() 与
与![]() 有公共点
有公共点![]() ,且在
,且在![]() 点处切线相同,求该切线方程;
点处切线相同,求该切线方程;
(Ⅱ)若函数![]() 有极值但无零点,求实数
有极值但无零点,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() ,
, ![]() 时,求
时,求![]() 在区间
在区间![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为6,且椭圆
的长轴长为6,且椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
, ![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形.若存在,求出点
为底边的等腰三角形.若存在,求出点![]() 的横坐标的取值范围,若不存在,请说明理由.
的横坐标的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斐波那契数列![]() 满足:
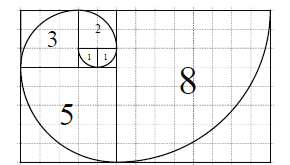
满足: ![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() .
.
(Ⅰ)若曲线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,求
处具有公共切线,求![]() ,
, ![]() 的值;
的值;
(Ⅱ)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 内恰有两个零点,求
内恰有两个零点,求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记函数f(x)=log2(2x﹣3)的定义域为集合M,函数g(x)=![]() 的定义域为集合N.求:
的定义域为集合N.求:
(Ⅰ)集合M,N;
(Ⅱ)集合M∩N,R(M∪N).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com