
 、
、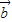 都是非零向量,则“
都是非零向量,则“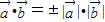 ”是“
”是“ 、
、 共线”的充要条件
共线”的充要条件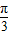 )的图象向右平移
)的图象向右平移 个单位,得到函数y=sin2x的图象;
个单位,得到函数y=sin2x的图象; ,则△ABC必为锐角三角形;
,则△ABC必为锐角三角形; 、
、 共线,则夹角θ=0或θ=π,代入向量的数量积的定义可得;反之,若
共线,则夹角θ=0或θ=π,代入向量的数量积的定义可得;反之,若 ,由向量的数量积的定义可知,夹角θ=0或θ=π,即
,由向量的数量积的定义可知,夹角θ=0或θ=π,即 、
、 共线(2)将函数y=sin(2x+
共线(2)将函数y=sin(2x+ )的图象向右平移
)的图象向右平移 个单位,得到函数y=sin2[(x-
个单位,得到函数y=sin2[(x- )+
)+ ]=sin(2x-
]=sin(2x- )的图象;(3)在△ABC中,由AB=2<AC=3,∠ABC=
)的图象;(3)在△ABC中,由AB=2<AC=3,∠ABC= ,可知C为锐角,由正弦定理可得
,可知C为锐角,由正弦定理可得 可求cosC=
可求cosC= 可知C为锐角,再由cosA=-cos(B+C)=-cosBcosC+sinBsinC>0可得A为锐角,(4)在同一坐标系中,函数y=sinx的图象和函数y=x的图象有1个公共点
可知C为锐角,再由cosA=-cos(B+C)=-cosBcosC+sinBsinC>0可得A为锐角,(4)在同一坐标系中,函数y=sinx的图象和函数y=x的图象有1个公共点 、
、 共线,则夹角θ=0或θ=π,从而
共线,则夹角θ=0或θ=π,从而 ;反之,若
;反之,若 ,由向量的数量积的定义可知,cosθ=±1,即θ=0或θ=π,即
,由向量的数量积的定义可知,cosθ=±1,即θ=0或θ=π,即 、
、 共线;故(1)正确
共线;故(1)正确 )的图象向右平移
)的图象向右平移 个单位,得到函数y=sin2[(x-
个单位,得到函数y=sin2[(x- )+
)+ ]=sin(2x-
]=sin(2x- )的图象;故(2)错误
)的图象;故(2)错误 ,可知C为锐角,由正弦定理可得
,可知C为锐角,由正弦定理可得 ⇒
⇒ =
= ,cosC=
,cosC= ,再由cosA=-cos(B+C)=-cosBcosC+sinBsinC>0可得A为锐角,故(3)正确
,再由cosA=-cos(B+C)=-cosBcosC+sinBsinC>0可得A为锐角,故(3)正确

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
| 1 |
| x 2-3x+2 |
| 1 |
| x 2-3x+2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com