
【题目】体温是人体健康状况的直接反应,一般认为成年人腋下温度![]() (单位:
(单位:![]() )平均在
)平均在![]() 之间即为正常体温,超过
之间即为正常体温,超过![]() 即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:
即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:![]() ;高热:
;高热:![]() ;超高热(有生命危险):
;超高热(有生命危险):![]() .
.
某位患者因患肺炎发热,于12日至26日住院治疗. 医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热. 住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:

(1)请你计算住院期间该患者体温不低于![]() 的各天体温平均值;
的各天体温平均值;
(2)在![]() 日—
日—![]() 日期间,医生会随机选取
日期间,医生会随机选取![]() 天在测量体温的同时为该患者进行某一特殊项目“
天在测量体温的同时为该患者进行某一特殊项目“![]() 项目”的检查,记
项目”的检查,记![]() 为高热体温下做“
为高热体温下做“![]() 项目”检查的天数,试求
项目”检查的天数,试求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)抗生素治疗一般在服药后2-8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果.假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() ;(3)答案不唯一,给出合理理由即可.
;(3)答案不唯一,给出合理理由即可.
【解析】
(1)由题意利用平均数公式直接求解即可;
(2)由题意利用超几何分布的概率公式即可分别求出![]() 、
、![]() 、
、![]() ,列出分布列后即可求期望;
,列出分布列后即可求期望;
(3)可从各抗生素降温总数,使用抗生素时体温平均值和方差,体温稳定下降的时间点和单日温度下降最大值几个角度去考虑,选出效果最佳的抗生素.
(1)由表可知,该患者共6天的体温不低于![]() ,记平均体温为
,记平均体温为![]() ,
,
![]() .
.
所以,患者体温不低于![]() 的各天体温平均值为
的各天体温平均值为![]() .
.
(2)![]() 的所有可能取值为
的所有可能取值为![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
则![]() 的分布列为:
的分布列为:
|
|
|
|
P |
|
|
|
所以![]() .
.
(3)“抗生素C”治疗效果最佳可使用理由:
①“抗生素B”使用期间先连续两天降温1.0![]() 又回升0.1
又回升0.1![]() ,“抗生素C”使用期间持续降温共计1.2
,“抗生素C”使用期间持续降温共计1.2![]() ,说明“抗生素C”降温效果最好,故“抗生素C”治疗效果最佳.
,说明“抗生素C”降温效果最好,故“抗生素C”治疗效果最佳.
②抗生素B”治疗期间平均体温39.03![]() ,方差约为
,方差约为![]() ;“抗生素C”平均体温38
;“抗生素C”平均体温38![]() ,方差约为
,方差约为![]() ,“抗生素C”治疗期间体温离散程度大,说明存在某个时间节点降温效果明显,故“抗生素C”治疗效果最佳.
,“抗生素C”治疗期间体温离散程度大,说明存在某个时间节点降温效果明显,故“抗生素C”治疗效果最佳.
“抗生素B”治疗效果最佳可使用理由:
自使用“抗生素B”开始治疗后,体温才开始稳定下降,且使用“抗生素B”治疗当天共降温0.7![]() ,是单日降温效果最好的一天,故“抗生素B”治疗效果最佳.
,是单日降温效果最好的一天,故“抗生素B”治疗效果最佳.


科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C的极坐标方程为![]() .以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
.以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为![]() (t为参数)
(t为参数)
(1)若![]() ,求曲线C的直角坐标方程以及直线l的极坐标方程;
,求曲线C的直角坐标方程以及直线l的极坐标方程;
(2)设点![]() ,曲线C与直线
,曲线C与直线![]() 交于A、B两点,求
交于A、B两点,求![]() 的最小值
的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: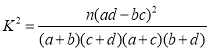 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的正确指导下,通过全国人民的齐心协力,特别是全体一线医护人员的奋力救治,二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下:

根据图中甲、乙两省的数字特征进行比对,通过比较把你得到最重要的两个结论写在答案纸指定的空白处.
①_________________________________________________.
②_________________________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,有以下三个结论:
,有以下三个结论:
①函数恒有两个零点,且两个零点之积为![]() ;
;
②函数的极值点不可能是![]() ;
;
③函数必有最小值.
其中正确结论的个数有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”.1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到2019这2019个数中,能被3除余2且被5整除余2的数按从小到大的顺序排成一列,构成数列![]() ,则此数列所有项中,中间项的值为( )
,则此数列所有项中,中间项的值为( )
A.992B.1022C.1007D.1037
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4 坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),并以
为参数),并以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)写出![]() 的极坐标方程,并将
的极坐标方程,并将![]() 化为普通方程;
化为普通方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() 与
与![]() 相交于
相交于![]() 两点,
两点,
求![]() 的面积(
的面积(![]() 为圆
为圆![]() 的圆心).
的圆心).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,若椭圆上一点
,若椭圆上一点![]() 满足
满足![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]()
![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作
作![]() 轴的垂线,交椭圆
轴的垂线,交椭圆![]() 于
于![]() ,求证:
,求证: ![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com