练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】【2018广东深圳市高三一模】已知椭圆的离心率为，直线与椭圆有且只有一个交点．

    （I）求椭圆的方程和点的坐标；

    （II） 为坐标原点，与平行的直线与椭圆交于不同的两点， ，求的面积最大时直线的方程．

    【答案】（I）椭圆的方程为，点的坐标为；（II）或．

    【解析】试题分析：(1) 根据椭圆的离心率为，直线与椭圆有且只有一个交点，结合性质 ，列出关于 、 、的方程组，求出 、 、，即可得结果；(2) 设直线的方程为，设， ，联立消去，利用韦达定理，弦长公式以及点到直线距离公式与三角形面积公式可得，利用二次函数的性质可得结果.

    试题解析：(1)由，得，故.

    则椭圆的方程为.

    由，消去，得.①

    由，得.

    故椭圆的方程为.

    所以，所以点的坐标为；

    (2)设直线的方程为，

    设， ，联立消去，得，

    则有，

    由，得，

    .

    设原点到直线的距离为.

    则.

    所以.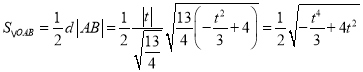

    所以当时，即时， 的面积最大.

    所以直线的方程为或.

    【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和数量积公式，属于难题.用待定系数法求椭圆方程的一般步骤；①作判断：根据条件判断椭圆的焦点在轴上，还是在轴上，还是两个坐标轴都有可能；②设方程：根据上述判断设方程或 ；③找关系：根据已知条件，建立关于、、的方程组；④得方程：解方程组，将解代入所设方程，即为所求.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设命题：实数满足，其中，命题：实数满足.

    （1）若，且为真，求实数的取值范围；

    （2）若是的充分不必要条件，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列所给4个图象中，与所给3件事吻合最好的顺序为 （ ）

    ①我离开学校不久，发现自己把作业本忘在教室，于是立刻返回教室里取了作业本再回家；

    ②我放学回家骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；

    ③我放学从学校出发后，心情轻松，缓缓行进，后来为了赶时间开始加速.

    A.（1）（2）（4）B.（4）（1）（2）C.（4）（1）（3）D.（4）（2）（3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒．为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x元．每笔订单顾客网上支付成功后，李明会得到支付款的80%．

    ①当x=10时，顾客一次购买草莓和西瓜各1盒，需要支付__________元；

    ②在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（xR），g（x）=2a-1

    （1）求函数f（x）的单调区间与极值．

    （2）若f（x）≥g（x）对恒成立，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在底面是正三角形的三棱锥中,D 为PC的中点，，

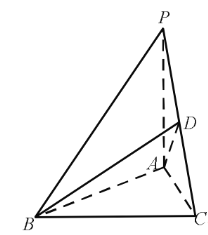
    （1）求证：平面 ；

    （2）求 BD 与平面 ABC 所成角的大小；

    （3）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校选派甲、乙、丙、丁、戊5名学生代表学校参加市级“演讲”和“诗词”比赛，下面是他们的一段对话．甲说：“乙参加‘演讲’比赛”；乙说：“丙参加‘诗词’比赛”；丙说“丁参加‘演讲’比赛”；丁说：“戊参加‘诗词’比赛”；戊说：“丁参加‘诗词’比赛”．

    已知这5个人中有2人参加“演讲”比赛，有3人参加“诗词”比赛，其中有2人说的不正确，且参加“演讲”的2人中只有1人说的不正确．根据以上信息，可以确定参加“演讲”比赛的学生是

    A. 甲和乙 B. 乙和丙 C. 丁和戊 D. 甲和丁

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    (1)当时，解不等式：；

    (2)当时，存在最小值，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，平面，点在以为直径的上，，，点为线段的中点，点在弧上，且.

    （1）求证：平面平面；

    （2）求证：平面平面；

    （3）设二面角的大小为，求的值.

    【答案】(1)证明见解析；(2)证明见解析；(3).

    【解析】试题分析：

    （1）由△ABC中位线的性质可得，则平面.由线面平行的判断定理可得平面.结合面面平行的判断定理可得平面.

    （2）由圆的性质可得，由线面垂直的性质可得，据此可知平面.利用面面垂直的判断定理可得平面平面.

    （3）以为坐标原点，所在的直线为轴，所在的直线为轴，建立空间直角坐标系.结合空间几何关系计算可得平面的法向量，平面的一个法向量，则.由图可知为锐角，故.

    试题解析：

    （1）证明：因为点为线段的中点，点为线段的中点，

    所以，因为平面，平面，所以平面.

    因为，且平面，平面，所以平面.

    因为平面，平面，，

    所以平面平面.

    （2）证明：因为点在以为直径的上，所以，即.

    因为平面，平面，所以.

    因为平面，平面，，所以平面.

    因为平面，所以平面平面.

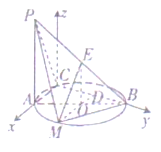
    （3）解：如图，以为坐标原点，所在的直线为轴，所在的直线为轴，建立空间直角坐标系.

    因为，，所以，.

    延长交于点.因为，

    所以，，.

    所以，，，.

    所以，.

    设平面的法向量.

    因为，所以，即.

    令，则，.

    所以.

    同理可求平面的一个法向量.

    所以.由图可知为锐角，所以.

    【题型】解答题
    【结束】
    21

    【题目】已知圆，点，直线.

    （1）求与圆相切，且与直线垂直的直线方程；

    （2）在直线上（为坐标原点），存在定点（不同于点），满足：对于圆上任一点，都有为一常数，试求所有满足条件的点的坐标.

    查看答案和解析>>

    同步练习册答案