
【题目】已知函数![]() 与
与![]() 的图象上存在关于
的图象上存在关于![]() 轴对称的点,则实数
轴对称的点,则实数![]() 的取值范围是_________.
的取值范围是_________.
【答案】![]()
【解析】
函数f(x)与g(x)图象上存在关于y轴对称的点,就是f(﹣x)=g(x)有解,也就是函数y=f(﹣x)与函数y=g(x)有交点,
在同一坐标系内画函数y=f(﹣x)![]() (x>0)与函数y=g(x)=ln(x+a)的图象,结合图象解题.
(x>0)与函数y=g(x)=ln(x+a)的图象,结合图象解题.
函数f(x)与g(x)图象上存在关于y轴有对称的点,
就是f(﹣x)=g(x)有解,
也就是函数y=f(﹣x)与函数y=g(x)有交点,
在同一坐标系内画函数y=f(﹣x)![]() (x>0)与函数y=g(x)=ln(x+a)的图象:
(x>0)与函数y=g(x)=ln(x+a)的图象:
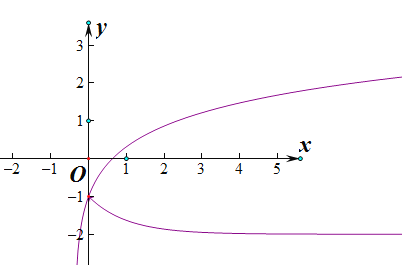
∴函数y=g(x)=ln(x+a)的图象是把由函数y=lnx的图象向左平移
且平移到过点(0,![]() )后开始,两函数的图象没有有交点,
)后开始,两函数的图象没有有交点,
把点(0,![]() )代入y=ln(x+a)得,
)代入y=ln(x+a)得,![]() lna,∴a
lna,∴a![]() ,
,
∴a![]() ,
,
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系.
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程![]() 的回归系数a,b;
的回归系数a,b;
(3)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线![]() 和
和![]() 是异面直线,
是异面直线,![]() 在平面
在平面![]() 内,
内,![]() 在平面
在平面![]() 内,
内,![]() 是平面
是平面![]() 与平面
与平面![]() 的交线,则下列命题正确的是( )
的交线,则下列命题正确的是( )
A. ![]() 与
与![]() 都不相交 B.
都不相交 B. ![]() 与
与![]() 都相交
都相交
C. ![]() 至多与
至多与![]() 中的一条相交 D.
中的一条相交 D. ![]() 至少与
至少与![]() 中的一条相交
中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】红星海水养殖场进行某水产品的新旧养殖方法的产量对比,收货时在旧养殖的大量网箱中随机抽取![]() 个网箱,在新养殖法养殖的大量网箱中也随机抽取
个网箱,在新养殖法养殖的大量网箱中也随机抽取![]() 个网箱,测量各箱水产品的产量,得样本频率分布直方图如下:
个网箱,测量各箱水产品的产量,得样本频率分布直方图如下:

(1)填写下列列联表,并根据列联表判断是否有![]() 的把握认为箱产量与养殖方法有关.
的把握认为箱产量与养殖方法有关.
养殖法 箱产量 | 箱产量 | 箱产量 | 总计 |
旧养殖法 | |||
新养殖法 | |||
总计 |
(2)设两种养殖方法的产量互相独立,记![]() 表示事件:“旧养殖法的箱产量低于
表示事件:“旧养殖法的箱产量低于![]() ,新养殖法的箱产量不低于
,新养殖法的箱产量不低于![]() ”,估计
”,估计![]() 的概率;
的概率;
(3)某水产批发户从红星海水养殖场用新养殖法养殖的大量网箱水产品中购买了![]() 个网箱的水产品,记
个网箱的水产品,记![]() 表示箱产量位于区间
表示箱产量位于区间![]() 的网箱个数,以上样本在相应区间的频率代替概率,求
的网箱个数,以上样本在相应区间的频率代替概率,求![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
(![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 在
在![]() 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求函数的解析式.
(2)求函数的单调递增区间.
(3)是否存在实数![]() ,满足不等式
,满足不等式![]() ?若存在,求出
?若存在,求出![]() 的范围(或值);若不存在,请说明理由.
的范围(或值);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难并不断加大对各国的施压,拉拢他们抵制华为5G,然而这并没有让华为却步.华为在2019年不仅净利润创下记录,海外增长同祥强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投人固定成本250万,每生产x(千部)手机,需另投入成本![]() 万元,且
万元,且 ,由市场调研知,每部手机售价0.8万元,且全年内生产的手机当年能全部销售完.
,由市场调研知,每部手机售价0.8万元,且全年内生产的手机当年能全部销售完.
(Ⅰ)求出2020年的利润![]() (万元)关于年产量x(千部)的函数关系式(利润=销售额-成本);
(万元)关于年产量x(千部)的函数关系式(利润=销售额-成本);
(Ⅱ)2020年产量x为多少(千部)时,企业所获利润最大?最大利润是多少?
(说明:当![]() 时,函数
时,函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增)
单调递增)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com