
(本小题13分)已知函数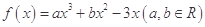 在点
在点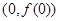 处的切线与直线
处的切线与直线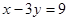 垂直.
垂直.
(1)若对于区间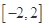 上任意两个自变量的值
上任意两个自变量的值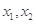 都有
都有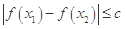 ,求实数
,求实数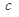 的最小值;
的最小值;
(2)若过点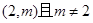 可作曲线
可作曲线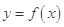 的三条切线,求实数
的三条切线,求实数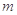 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值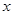 (单位:元,
(单位:元,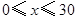 )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成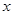 的函数;(II)如何定价才能使一个星期的商品销售利润最大?
的函数;(II)如何定价才能使一个星期的商品销售利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是 (万元)和
(万元)和 (万元),它们与投入资金
(万元),它们与投入资金 (万元)的关系有经验公式:
(万元)的关系有经验公式: 。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共8分)
提高二环路的车辆通行能力可有效改善整个城区的交通状况,在一般情况下,二环路上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数。当二环路上的车流密度达到600辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过60辆/千米时,车流速度为80千米/小时,研究表明:当60≤x≤600时,车流速度v是车流密度x的一次函数。
(Ⅰ)当0≤x≤600时,求函数f(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过二环路上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值。(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)已知函数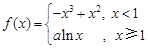 ,其中
,其中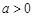
(Ⅰ)求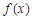 在
在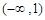 上的单调区间;
上的单调区间;
(Ⅱ)求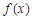 在
在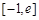 (
(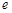 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;
(III)对任意给定的正实数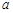 ,曲线
,曲线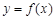 上是否存在两点
上是否存在两点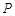 、
、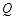 ,使得
,使得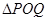 是以原点
是以原点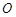 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在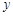 轴上?
轴上?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
某网店对一应季商品过去20天的销售价格及销售量进行了监测统计发现,第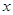 天(
天(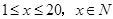 )的销售价格(单位:元)为
)的销售价格(单位:元)为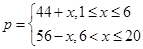 ,第
,第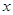 天的销售量为
天的销售量为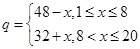 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元.
(Ⅰ)写出销售额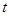 关于第
关于第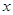 天的函数关系式;
天的函数关系式;
(Ⅱ)求该商品第7天的利润;
(Ⅲ)该商品第几天的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 为常数,且
为常数,且 )满足条件:
)满足条件: ,且方程
,且方程 有两个相等的实数根.
有两个相等的实数根.
(1)求 的解析式;
的解析式;
(2)求函数在区间 上的最大值和最小值;
上的最大值和最小值;
(3)是否存在实数
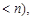 使
使 的定义域和值域分别为
的定义域和值域分别为 和
和 ,如果存在,求出
,如果存在,求出 的值,如不存在,请说明理由.
的值,如不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率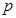 与每日生产产品件数
与每日生产产品件数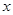 (
(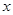

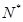 )间的关系为
)间的关系为 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
(注:正品率=产品的正品件数÷产品总件数×100%)
(1)将日利润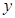 (元)表示成日产量
(元)表示成日产量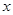 (件)的函数;
(件)的函数;
(2)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com