
【题目】【2018安徽淮南市高三一模(2月)】已知函数![]() .
.
(I)若![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(II)曲线![]() 与直线
与直线![]() 交于
交于![]() ,
, ![]() 两点,其中
两点,其中![]() ,若直线
,若直线![]() 斜率为
斜率为![]() ,求证:
,求证: ![]() .
.
【答案】(I)答案见解析;(II)证明见解析.
【解析】试题分析:(1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)问题等价于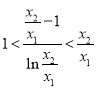 ,令
,令![]() ,则
,则![]() ,问题转化为只需证
,问题转化为只需证![]() ,根据函数的单调性证明即可.
,根据函数的单调性证明即可.
试题解析:
(1) ![]() ,
, ![]() ,
,
当![]() 时,恒有
时,恒有![]() ,
, ![]() 在区间
在区间![]() 上是增函数,
上是增函数,
当![]() 时,令
时,令![]() ,即
,即![]() ,解得
,解得![]() ;令
;令![]() ,即
,即![]() ,解得
,解得![]() ,
, ![]() 在区间
在区间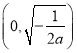 上是增函数,在区间
上是增函数,在区间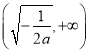 上是减函数.
上是减函数.
综上,当![]() 时,
时, ![]() 在区间
在区间![]() 上是增函数;
上是增函数;
当![]() 时,
时, ![]() 在区间
在区间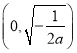 上是增函数,在区间
上是增函数,在区间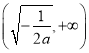 上是减函数.
上是减函数.
(2)证明: ![]() ,要证明
,要证明![]() ,
,
即证![]() ,等价于
,等价于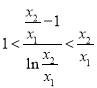 ,令
,令![]() (由
(由![]() ,知
,知![]() ),
),
则只需证![]() ,由
,由![]() 知
知![]() ,故等价于
,故等价于![]() (*)
(*)
①令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
当![]() 时,
时, ![]() ,所以
,所以![]() ;
;
②令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 内是增函数,
内是增函数,
当![]() 时,
时, ![]() ,所以
,所以![]() ,
,
综上, ![]() .
.


科目:高中数学 来源: 题型:
【题目】某电视台问政直播节目首场内容是“让交通更顺畅”.A、B、C、D四个管理部门的负责人接受问政,分别负责问政A、B、C、D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)人数的条形图如下.为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价,对每位现场市民都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A部门 | 50% | 25% | 25% |
B部门 | 80% | 0 | 20% |
C部门 | 50% | 50% | 0 |
D部门 | 40% | 20% | 40% |

(1)若市民甲选择的是A部门,求甲的调查问卷被选中的概率;
(2)若想从调查问卷被选中且填写不满意的市民中再选出2人进行电视访谈,求这两人中至少有一人选择的是D部门的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() 的短轴为
的短轴为![]() ,
,![]() ,离心率
,离心率![]() ,
,![]() 为第一象限内椭圆上的任意一点,设
为第一象限内椭圆上的任意一点,设![]() 轴于
轴于![]() ,
,![]() 为线段
为线段![]() 的中点,过
的中点,过![]() 作直线
作直线![]() 轴.
轴.
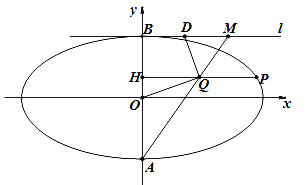
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 的纵坐标为
的纵坐标为![]() ,求直线
,求直线![]() 截椭圆
截椭圆![]() 所得的弦长;
所得的弦长;
(3)若直线![]() 交直线
交直线![]() 于
于![]() ,
,![]() 为直线
为直线![]() 上一点,且
上一点,且![]() 为原点),证明:
为原点),证明:![]() 为线段
为线段![]() 的中点.
的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点 ,且两焦点与短轴的一个端点构成等腰直角三角形.
,且两焦点与短轴的一个端点构成等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)若圆![]() 的任意一条切线
的任意一条切线![]() 与椭圆E相交于P,Q两点,试问:
与椭圆E相交于P,Q两点,试问: ![]() 是否为定值? 若是,求这个定值;若不是,说明理由.
是否为定值? 若是,求这个定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.2018年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本2500万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且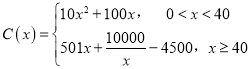 .由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
.由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点, ![]() 为
为![]() 上的任意一点.
上的任意一点.
(1)求![]() 的取值范围;
的取值范围;
(2)![]() 是
是![]() 上异于
上异于![]() 的两点,若直线
的两点,若直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,证明:
,证明: ![]() 两点的横坐标之和为常数.
两点的横坐标之和为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
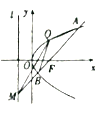
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,抛物线上一定点
,抛物线上一定点![]() .
.
(1)求抛物线![]() 的方程及准线
的方程及准线![]() 的方程;
的方程;
(2)过焦点![]() 的直线(不经过
的直线(不经过![]() 点)与抛物线交于
点)与抛物线交于![]() 两点,与准线
两点,与准线![]() 交于点
交于点![]() ,记
,记![]() 的斜率分别为
的斜率分别为![]() ,问是否存在常数
,问是否存在常数![]() ,使得
,使得![]() 成立?若存在
成立?若存在![]() ,求出
,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com