
椭圆 的右焦点为
的右焦点为 ,右准线为
,右准线为 ,离心率为
,离心率为 ,点
,点 在椭圆上,以
在椭圆上,以 为圆心,
为圆心, 为半径的圆与
为半径的圆与 的两个公共点是
的两个公共点是 .
.

(1)若 是边长为
是边长为 的等边三角形,求圆的方程;
的等边三角形,求圆的方程;
(2)若 三点在同一条直线
三点在同一条直线 上,且原点到直线
上,且原点到直线 的距离为
的距离为 ,求椭圆方程.
,求椭圆方程.
(1) 。(2)
。(2) .
.
【解析】
试题分析:设椭圆的半长轴是 ,半短轴是
,半短轴是 ,半焦距离是
,半焦距离是 ,
,
由椭圆 的离心率为
的离心率为 ,可得椭圆
,可得椭圆 方程是
方程是 ,
2分
,
2分
(只要是一个字母,其它形式同样得分,)
焦点 ,准线
,准线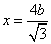 ,设点
,设点 ,
,
(1) 是边长为
是边长为 的等边三角形,
的等边三角形,
则圆半径为 ,且
,且 到直线
到直线 的距离是
的距离是 ,
,
又 到直线
到直线 的距离是
的距离是 ,
,
所以, ,
, ,所以
,所以
所以,圆的方程是 。
6分
。
6分
(2)因为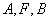 三点共线,且
三点共线,且 是圆心,所以
是圆心,所以 是线段
是线段 中点,
中点,
由 点横坐标是
点横坐标是 得,
得, ,
8分
,
8分
再由 得:
得: ,
, ,
,
所以直线 斜率
斜率 10分
10分
直线 :
: ,
, 12分
12分
原点 到直线
到直线 的距离
的距离 ,
,
依题意 ,
, ,所以
,所以 ,
,
所以椭圆的方程是 .
15分
.
15分
考点:本题考查了圆与椭圆
点评:解答此类综合题时,应根据其几何特征熟练的转化为数量关系(如方程、函数),再结合代数方法解答,这就要学生在解决问题时要充分利用数形结合、设而不求、弦长公式及韦达定理综合思考,重视对称思想、函数与方程思想、等价转化思想的应用


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
| a2+b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 6 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com