
【题目】已知椭圆 ![]() 上两个不同的点A,B关于直线y=mx+
上两个不同的点A,B关于直线y=mx+ ![]() 对称.
对称. 
(1)求实数m的取值范围;
(2)求△AOB面积的最大值(O为坐标原点).
【答案】
(1)解:由题意,可设直线AB的方程为x=﹣my+n,代入椭圆方程 ![]() ,可得(m2+2)y2﹣2mny+n2﹣2=0,
,可得(m2+2)y2﹣2mny+n2﹣2=0,
设A(x1,y1),B(x2,y2).由题意,△=4m2n2﹣4(m2+2)(n2﹣2)=8(m2﹣n2+2)>0,
设线段AB的中点P(x0,y0),则 ![]() .x0=﹣m×
.x0=﹣m× ![]() +n=
+n= ![]() ,
,
由于点P在直线y=mx+ ![]() 上,∴
上,∴ ![]() =
= ![]() +
+ ![]() ,
,
∴ ![]() ,代入△>0,可得3m4+4m2﹣4>0,
,代入△>0,可得3m4+4m2﹣4>0,
解得m2 ![]() ,∴
,∴ ![]() 或m
或m ![]()
(2)解:直线AB与x轴交点横坐标为n,
∴S△OAB= ![]() =
= ![]() |n|
|n| ![]() =
= ![]() ,
,
由均值不等式可得:n2(m2﹣n2+2) ![]() =
= ![]() ,
,
∴S△AOB ![]() =
= ![]() ,当且仅当n2=m2﹣n2+2,即2n2=m2+2,又∵
,当且仅当n2=m2﹣n2+2,即2n2=m2+2,又∵ ![]() ,解得m=
,解得m= ![]() ,
,
当且仅当m= ![]()
![]()
【解析】(1)由题意,可设直线AB的方程为x=﹣my+n,代入椭圆方程可得(m2+2)y2﹣2mny+n2﹣2=0,设A(x1 , y1),B(x2 , y2).可得△>0,设线段AB的中点P(x0 , y0),利用中点坐标公式及其根与系数的可得P,代入直线y=mx+ ![]() ,可得
,可得 ![]() ,代入△>0,即可解出.(2)直线AB与x轴交点横坐标为n,可得S△OAB=
,代入△>0,即可解出.(2)直线AB与x轴交点横坐标为n,可得S△OAB= ![]() ,再利用均值不等式即可得出.
,再利用均值不等式即可得出.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,D在AB上,AD:DB=1:2,E为AC中点,CD、BE相交于点P,连结AP.设 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),则x,y的值分别为( )
(x,y∈R),则x,y的值分别为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() ),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
A.[ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
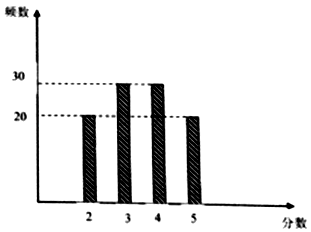
【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.
(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;
(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).
(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).
服务质量评分X | X≤5 | 6≤X≤8 | X≥9 |
等级 | 不好 | 较好 | 优良 |
奖惩标准(元) | ﹣1000 | 2000 | 3000 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要测量电视塔AB的高度,在C点测得塔顶的仰角是45°,在D点测得塔顶的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度是( )
A.30m
B.40m
C.![]() m
m
D.![]() m
m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x﹣ ![]() )+2cos2x,将函数y=f(x)的图象向右平移
)+2cos2x,将函数y=f(x)的图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
A.(﹣ ![]() ,1)
,1)
B.(﹣ ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数,﹣π<α<0),曲线C2的参数方程为
(α为参数,﹣π<α<0),曲线C2的参数方程为  (t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1的极坐标方程和曲线C2的普通方程;
(2)射线θ=﹣ ![]() 与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)短轴的端点P(0,b)、Q(0,﹣b),长轴的一个端点为M,AB为经过椭圆中心且不在坐标轴上的一条弦,若PA、PB的斜率之积等于﹣
(a>b>0)短轴的端点P(0,b)、Q(0,﹣b),长轴的一个端点为M,AB为经过椭圆中心且不在坐标轴上的一条弦,若PA、PB的斜率之积等于﹣ ![]() ,则P到直线QM的距离为
,则P到直线QM的距离为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com