
(07年四川卷文)(12分)如图,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与直线
与直线![]() 所成的角为60°,又
所成的角为60°,又![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求多面体![]() 的体积.
的体积.
解析:本题主要考查异面直线所成的角、平面与平面垂直、二面角、棱锥体积等有关知识,考查思维能力和空间想象能力、应用向量知识解决数学问题的能力、化归转化能力和推理运算能力.
(Ⅰ)∵平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
∴![]() 平面
平面![]()
又∵![]() 平面
平面![]()
∴![]()
(Ⅱ)取![]() 的中点
的中点![]() ,则
,则![]() .连接
.连接![]() 、
、![]() .
.
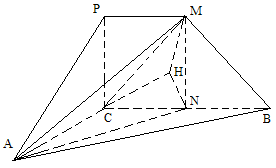
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() .
.
∴![]() 平面
平面![]() .
.
∵![]() ,∴
,∴![]() ,从而
,从而![]() 平面
平面![]() .
.
作![]() 于
于![]() ,连结
,连结![]() ,则由三垂线定理知
,则由三垂线定理知![]() .
.
从而![]() 为二面角
为二面角![]() 的平面角.
的平面角.
∵直线![]() 与直线
与直线![]() 所成的角为60°,
所成的角为60°,
∴![]() .
.
在![]() 中,由勾股定理得
中,由勾股定理得![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,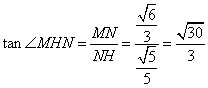
故二面角![]() 的大小为
的大小为![]()
(Ⅱ)如图以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .
.
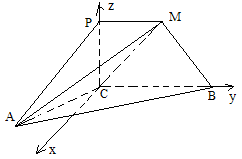
设![]()
![]() ,
,
有![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]()
由直线![]() 与直线
与直线![]() 所成的角为60°,得
所成的角为60°,得
![]()
即![]() ,解得
,解得![]() .
.
∴![]() ,
,![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
由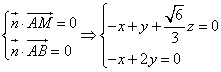 ,取
,取![]() ,得
,得![]()
取平面![]() 的一个法向量为
的一个法向量为![]()
则![]()
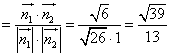
由图知二面角![]() 为锐二面角,
为锐二面角,
故二面角![]() 的大小为
的大小为![]() .
.
(Ⅲ)多面体![]() 就是四棱锥
就是四棱锥![]()


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com