
| x |
| a |
| y |
| b |


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013届安徽省屯溪一中高三第一次质量检测理科数学试卷(带解析) 题型:填空题
给出如下四个结论:
① 若“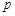 且
且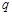 ”为假命题,则
”为假命题,则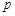 、
、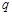 均为假命题;
均为假命题;
② 命题“若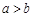 ,则
,则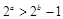 ”的否命题为“若
”的否命题为“若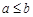 ,则
,则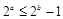 ”;
”;
③ 若随机变量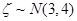 ,且
,且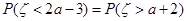 ,则
,则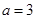 ;
;
④ 过点A(1,4),且横纵截距的绝对值相等的直线共有2条.
其中正确结论的序号是______________________________.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三第一次质量检测理科数学试卷(解析版) 题型:填空题
给出如下四个结论:
① 若“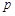 且
且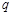 ”为假命题,则
”为假命题,则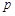 、
、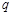 均为假命题;
均为假命题;
② 命题“若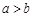 ,则
,则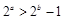 ”的否命题为“若
”的否命题为“若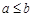 ,则
,则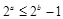 ”;
”;
③ 若随机变量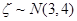 ,且
,且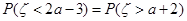 ,则
,则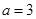 ;
;
④ 过点A(1,4),且横纵截距的绝对值相等的直线共有2条.
其中正确结论的序号是______________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com