
����Ŀ��ij���ӹ�˾����һ�������ֻ��������ÿ������ijɱ���15Ԫ�����ۼ���20Ԫ����ƽ������![]() ����ͨ���Ľ����գ�ÿ������ijɱ����䣬�����ͼ�����������ߣ��г������Ľ�����������ÿ����������ۼ���ߵİٷ���Ϊ
����ͨ���Ľ����գ�ÿ������ijɱ����䣬�����ͼ�����������ߣ��г������Ľ�����������ÿ����������ۼ���ߵİٷ���Ϊ![]() ����ô��ƽ�����������ٵİٷ���Ϊ
����ô��ƽ�����������ٵİٷ���Ϊ![]() ���ǸĽ����պ���ӹ�˾���۸��������ƽ��������
���ǸĽ����պ���ӹ�˾���۸��������ƽ��������![]() ��Ԫ��.
��Ԫ��.
��1���![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2���Ľ����պ���ȷ���������ֻ�������ۼۣ�ʹ���ӹ�˾���۸��������ƽ���������.
���𰸡�(1) ![]() ��
��![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ;(2) �Ľ����պ�ÿ����������ۼ�Ϊ
;(2) �Ľ����պ�ÿ����������ۼ�Ϊ![]() Ԫʱ���õ��ӹ�˾���۸��������ƽ���������.
Ԫʱ���õ��ӹ�˾���۸��������ƽ���������.
�������������������I��������֪ÿ����Ʒ�����ۼ�Ϊ![]() ������ƽ��������Ϊa
������ƽ��������Ϊa![]() �����������Ƕ��ߵĻ�ȥ���ɱ����ɣ�
�����������Ƕ��ߵĻ�ȥ���ɱ����ɣ�
��II���ɣ�1����֪����������һԪ���κ�����ϵ�����Զ����������ֵ��
���������
��I���Ľ����պ�ÿ����������ۼ�Ϊ![]() ����ƽ��������Ϊ
����ƽ��������Ϊ![]() ����
����
����ƽ������![]() ��Ԫ����
��Ԫ����
![]()
![]() ��
��![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]()
��II����![]() ��
��![]() ���ᣩ
���ᣩ
��![]() ʱ
ʱ![]() ��
�� ![]() ʱ
ʱ![]() ��
��
![]() ����
����![]() ��
��![]() ȡ�����ֵ��
ȡ�����ֵ��
�ʸĽ����պ�ÿ����������ۼ�Ϊ![]() Ԫʱ��
Ԫʱ��
�õ��ӹ�˾���۸��������ƽ���������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��
�� ![]() ��Բ
��Բ![]() ��
�� ![]() ��
��![]() ���ཻ��
���ཻ��![]() ��
��![]() ��
��![]() ��
��![]() �ĸ��㣮
�ĸ��㣮
������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�����ı���![]() ��������ʱ����Խ���
��������ʱ����Խ���![]() ��
��![]() �Ľ���
�Ľ���![]() �����꣮
�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ��U=R������A={x|��1��x��3}��B={x|2x��4��x��2}��
��1����U��A��B����
��2��������C={x|2x+a��0}������B��C=C����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
������![]() ����
����![]() 1��
1�� ![]() ��
�� ![]() ��
��
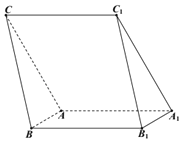
������֤�� ![]() ��
��
����������![]() �IJ������
�IJ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���f��x��=ax2+bx+c��a��0����ͼ����㣨0��1������x����Ψһ�Ľ��㣨��1��0���� ������f��x���ı���ʽ��
�����ڣ��������£��躯��F��x��=f��x����mx����F��x��������[��2��2]���ǵ�����������ʵ��m��ȡֵ��Χ��
�����躯��g��x��=f��x����kx��x��[��2��2]���Ǵ˺�������СֵΪh��k������h��k���Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ʵؾ��ȵ�����������ĸ����Ϸֱ��ʾ������1��2��3��4��һ���ʵؾ��ȵ����ӣ������壩���������Ϸֱ��ʾ����1��2��3��4��5��6���Ⱥ�����һ���������������.
��1���оٳ�ȫ�������¼���
��2����ѹ�ڵײ�����������֮��С��5�ĸ��ʣ�
��3�������������ϱ�ѹס�����ֲ�С�������ϱ�ѹס�����ֵĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ�У���֪����![]() �IJ�������Ϊ
�IJ�������Ϊ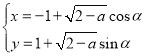 ��
��![]() ������
������![]() ����
����
����![]() ʱ��������
ʱ��������![]() �ϴ���
�ϴ���![]() ������ڵ�
������ڵ�![]() �����ĶԳƣ���ֱ��
�����ĶԳƣ���ֱ��![]() �IJ������̣�
�IJ������̣�
��������ԭ��Ϊ���㣬![]() ��������Ϊ����ļ�����ϵ�У������귽��Ϊ
��������Ϊ����ļ�����ϵ�У������귽��Ϊ![]() ��ֱ��
��ֱ��![]() ������
������![]() �ཻ��
�ཻ��![]() ���㣬��
���㣬��![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() ����Ϊ
����Ϊ![]() ����
����![]() ����Բ
����Բ![]() ����������˵㣬
����������˵㣬![]() ����Բ
����Բ![]() �ij�����˵㣮
�ij�����˵㣮
����![]() ʱ�����
ʱ�����![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ��
��![]() ����ֱ��
����ֱ��![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
����![]() ʱ��������
ʱ��������![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ���㣬OΪ����ԭ�㣬��
���㣬OΪ����ԭ�㣬��![]() ��
��![]() �����֮������ֵ��
�����֮������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
�� ![]() ��Ϊ�溯�������������Գ����ľ���Ϊ
��Ϊ�溯�������������Գ����ľ���Ϊ![]() .
.
��1����![]() ʱ����
ʱ����![]() �ĵ����ݼ����䣻
�ĵ����ݼ����䣻
��2��������![]() ��ͼ����
��ͼ����![]() �᷽������ƽ��
�᷽������ƽ��![]() ����λ���ȣ��ٰѺ��������̵�ԭ����
����λ���ȣ��ٰѺ��������̵�ԭ����![]() �������겻�䣩���õ�����
�������겻�䣩���õ�����![]() ��ͼ��.��
��ͼ��.��![]() ʱ������
ʱ������![]() ��ֵ��.
��ֵ��.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com