
为了调查某大学学生在周日上网的时间,随机对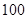 名男生和
名男生和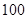 名女生进行了不记名的问卷调查,得到了如下的统计结果:
名女生进行了不记名的问卷调查,得到了如下的统计结果:
表1:男生上网时间与频数分布表
| 上网时间(分钟) | 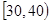 | 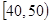 | 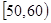 |  | 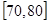 |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | 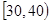 | 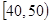 | 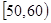 |  | 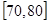 |
| 人数 | 10 | 20 | 40 | 20 | 10 |
 列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |
 ,其中
,其中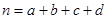
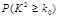 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
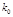 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
(I)225; (II)否;(III)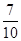 .
.
解析试题分析:(I)统计得到女生样本中的上网时间不少于60分钟的频数,根据频数与容量之比等于频率,易得到全校上网时间不少于60分钟的人数; (II)由以上列联表1、2的数据,可统计得到表3的数据,根据独立性检验原理可知:没有90%的把握认为“学生周日上网时间与性别有关”;(III) 五名男生中任取两人的基本事件数10个,根据表3可知男生上网超过60分钟与不超过60分钟的人数比为3:2,再写出至少一人超过60分钟的事件数7个,易求得概率为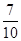 .
.
试题解析:(1)设估计上网时间不少于60分钟的人数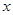 ,
,
依据题意有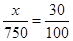 ,解得:
,解得: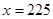 ,
,
所以估计其中上网时间不少于60分钟的人数是225人.
(2)根据题目所给数据得到如下列联表: 上网时间少于60分钟 上网时间不少于60分钟 合计 男生 60 40 100 女生 70 30 100 合计 130 70 200
其中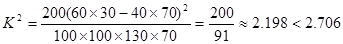 ,
,
因此,没有90%的把握认为“学生周日上网时间与性别有关”.
(3)因为上网时间少于60分钟与上网时间不少于60分钟的人数之比为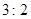 ,所以5人中上网时间少于60分钟的有3人,记为
,所以5人中上网时间少于60分钟的有3人,记为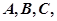 上网时间不少于60分钟的有2人,记为
上网时间不少于60分钟的有2人,记为 从中任取两人的所有基本事件为:(
从中任取两人的所有基本事件为:( ),(
),(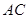 ),(
),(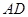 ),(
),(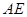 ),(
),(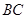 ),(
),(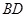 ),(
),(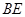 ),(
),(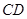 ),(
),( ),(
),(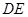 ),共10种,
),共10种,
其中“至少有一人上网时间超过60分钟”包含了7种,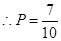 .
.
考点:1、用样本估计总体; 2、独立性检验;3、古典概型的概率求法.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
为预防H7N9病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
| 分组 | A组 | B组 | C组 |
| 疫苗有效 | 673 | a | b |
| 疫苗无效 | 77 | 90 | c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 |  |
| B | 12 | 3 |
| C | 8 | 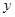 |
 与
与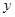 的值;
的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高三期末统一测试,随机抽取一部分学生的数学成绩分组统计如下表:
(Ⅰ)求出表中 、
、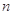 、
、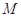 、
、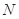 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
| 分组 | 频数 | 频率 |
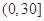 | 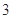 | 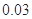 |
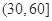 | 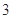 | 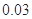 |
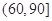 | 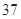 | 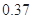 |
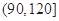 |  | 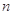 |
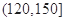 | 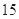 | 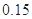 |
| 合计 | 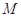 | 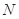 |

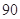 分以上的人数;
分以上的人数;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
南昌市为增强市民的交通安全意识,面向全市征召“小红帽”志愿者在部分交通路口协助交警维持交通,把符合条件的1000名志愿者按年龄分组:第1组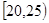 、第2组
、第2组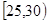 、第3组
、第3组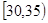 、第4组
、第4组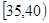 、第5组
、第5组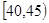 ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
(1)若从第3、4、5组中用分层抽样的方法抽取12名志愿者在五一节这天到广场协助交警维持交通,应从第3、4、5组各抽取多少名志愿者?
(2)在(1)的条件下,南昌市决定在这12名志愿者中随机抽取3名志愿者到学校宣讲交通安全知识,若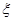 表示抽出的3名志愿者中第3组的人数,求
表示抽出的3名志愿者中第3组的人数,求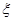 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种报纸,进货商当天以每份进价 元从报社购进,以每份售价
元从报社购进,以每份售价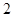 元售出。若当天卖不完,剩余报纸报社以每份
元售出。若当天卖不完,剩余报纸报社以每份 元的价格回收。根据市场统计,得到这个季节的日销售量
元的价格回收。根据市场统计,得到这个季节的日销售量 (单位:份)的频率分布直方图(如图所示),将频率视为概率。
(单位:份)的频率分布直方图(如图所示),将频率视为概率。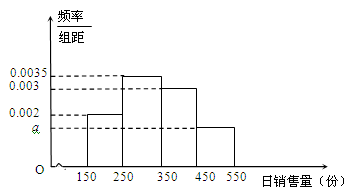
(Ⅰ)求频率分布直方图中 的值;
的值;
(Ⅱ)若进货量为 (单位:份),当
(单位:份),当

 时,求利润
时,求利润 的表达式;
的表达式;
(Ⅲ)若当天进货量 ,求利润
,求利润 的分布列和数学期望
的分布列和数学期望 (统计方法中,同一组数据常用该组区间的中点值作为代表).
(统计方法中,同一组数据常用该组区间的中点值作为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2012年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类: 第一类的用电区间在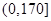 ,第二类在
,第二类在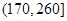 ,第三类在
,第三类在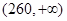 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示. 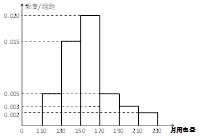
⑴ 求该小区居民用电量的中位数与平均数;
⑵ 利用分层抽样的方法从该小区内选出10位居民代表,若从该10户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率;
⑶ 若该小区长期保持着这一用电消耗水平,电力部门为鼓励其节约用电,连续10个月,每个月从该小区居民中随机抽取1户,若取到的是第一类居民,则发放礼品一份,设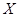 为获奖户数,求
为获奖户数,求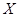 的数学期望
的数学期望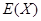 与方差
与方差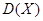 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有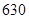 名学生,男女生人数之比为
名学生,男女生人数之比为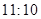 ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为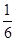 .
.
(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下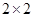 列联表:
列联表:
| | 否定 | 肯定 | 总计 |
| 男生 | | 10 | |
| 女生 | 30 | | |
| 总计 | | | |
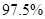 的把握认为态度与性别有关?
的把握认为态度与性别有关?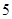 名男生被抽到,其中
名男生被抽到,其中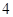 人持否定态度,
人持否定态度, 人持肯定态度;二班有
人持肯定态度;二班有 名女生被抽到,其中
名女生被抽到,其中 人持否定态度,
人持否定态度, 人持肯定态度.
人持肯定态度. 人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.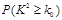 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
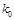 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下: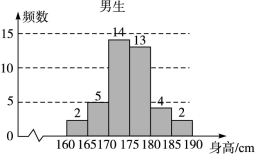
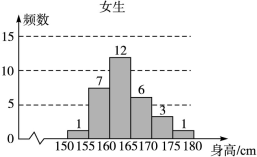
(Ⅰ)估计该校男生的人数;
(Ⅱ)估计该校学生身高在170~185 cm之间的概率;
(Ⅲ)从样本中身高在180~190 cm之间的男生中任选2人,求至少有1人身高在185~190 cm之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com