
【题目】如图,![]() 、
、![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() :
:![]() 的左、右焦点,过
的左、右焦点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 所得弦长为
所得弦长为![]() ,设
,设![]() 、
、![]() 是椭圆
是椭圆![]() 上的两个动点,线段
上的两个动点,线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 的横坐标为1.
的横坐标为1.
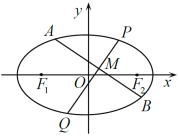
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知如图,长方体![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,过点
的中点,过点![]() 的平面
的平面![]() 与平面
与平面![]() 平行,且与长方体的面相交,交线围成一个几何图形.
平行,且与长方体的面相交,交线围成一个几何图形.
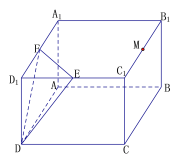
(1)在图中画出这个几何图形,并求这个几何图形的面积(画图说出作法,不用说明理由);
(2)求证:![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用![]() 局
局![]() 胜制(即先胜
胜制(即先胜![]() 局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以![]() 比
比![]() 获胜的概率;
获胜的概率;
(2)求乙获胜且比赛局数多于![]() 局的概率;
局的概率;
(3)求比赛局数![]() 的分布列,并求
的分布列,并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为![]() 的透明密闭的正方形容器
的透明密闭的正方形容器![]() 中,装有容器总体积一半的水(不计容器壁的厚度),将该正方体容器绕
中,装有容器总体积一半的水(不计容器壁的厚度),将该正方体容器绕![]() 旋转,并始终保持
旋转,并始终保持![]() 所在直线与水平平面平行,则在旋转过程中容器中水的水面面积的最大值为__________.
所在直线与水平平面平行,则在旋转过程中容器中水的水面面积的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 中,
中,![]() ,对任意正整数
,对任意正整数![]() ,
, .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比q的值,若不存在,请说明理由;
及公比q的值,若不存在,请说明理由;
(3)求数列![]() 前n项和
前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程![]() 的曲线即为函数
的曲线即为函数![]() 的图象,对于函数
的图象,对于函数![]() ,有如下结论:①
,有如下结论:①![]() 在
在![]() 上单调递减;②函数
上单调递减;②函数![]() 存在零点;③函数
存在零点;③函数![]() 的值域是R;④若函数
的值域是R;④若函数![]() 和
和![]() 的图象关于原点对称,则函数
的图象关于原点对称,则函数![]() 的图象就是
的图象就是![]() 确定的曲线
确定的曲线
其中所有正确的命题序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志是“连续10天,每天新增疑似病例不超过7人”,根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A. 甲地:总体均值为3,中位数为4
B. 乙地:总体均值为1,总体方差大于0
C. 丙地:总体均值为2,总体方差为3
D. 丁地:中位数为2,众数为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会为了解高二年级600名学生课余时间参加中华传统文化活动的情况(每名学生最多参加7场).随机抽取50名学生进行调查,将数据分组整理后,列表如下:

则以下四个结论中正确的是( )
A.表中![]() 的数值为10
的数值为10
B.估计该年级参加中华传统文化活动场数不高于2场的学生约为108人
C.估计该年级参加中华传统文化活动场数不低于4场的学生约为216人
D.若采用系统抽样方法进行调查,从该校高二600名学生中抽取容量为30的样本,则分段间隔为15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com